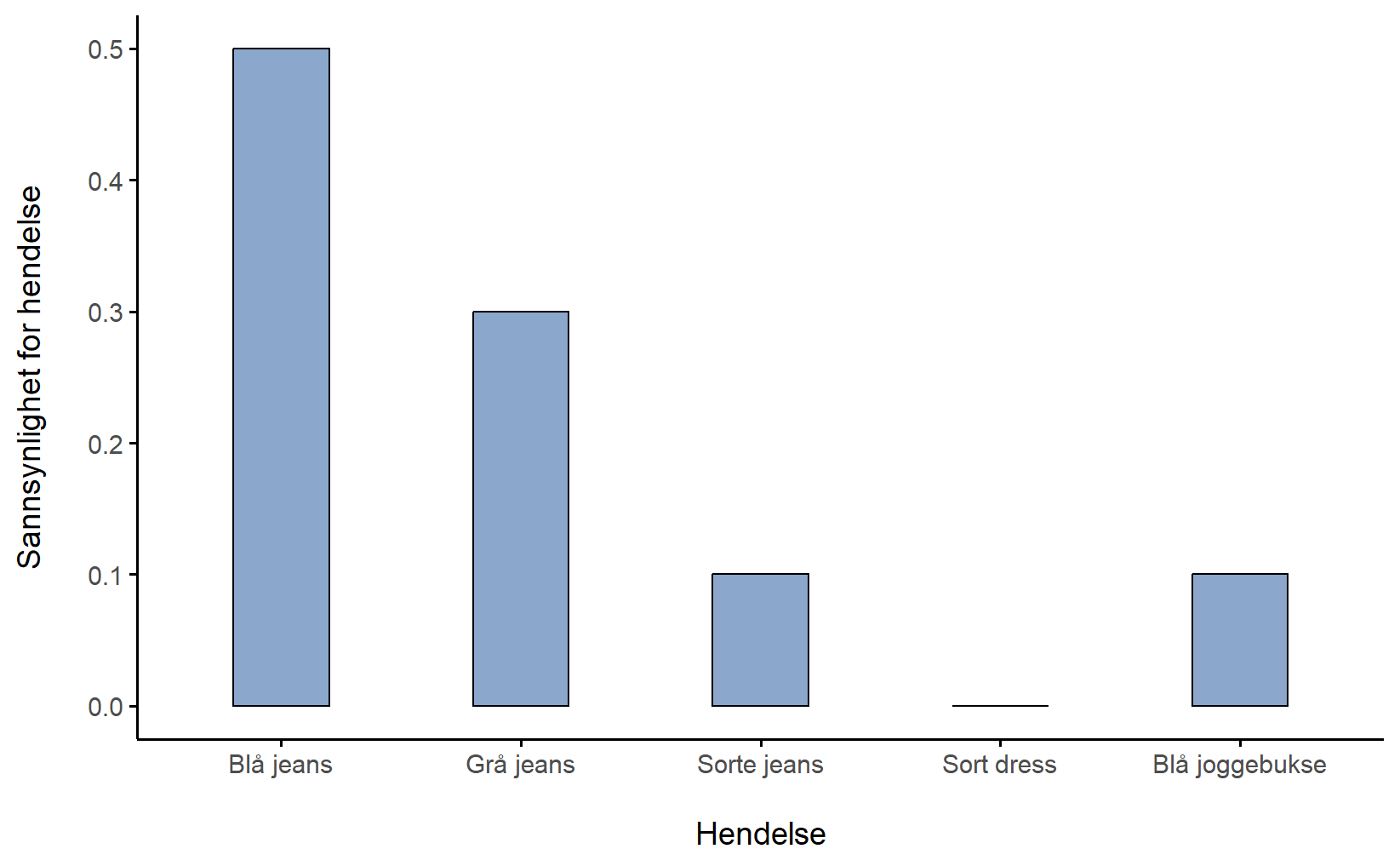6  Sannsynlighet

[God] has afforded us only the twilight … of Probability.
– John Locke

Så langt i boken har vi diskutert de mest grunnleggende temaene innen forskningsdesign, spesielt måling av konstrukter, og vi har vist hvordan man kan analysere innholdet i et datasett på en god måte. Jeg tror at for mange er det dette statistikk handler: samle inn tallene, regne ut gjennomsnitt, lage fine figurer og pakke alt sammen i en rapport. Litt som frimerkesamling, bare med tall i stedet!

Men statistikk er mye mer omfattende enn dette. Deskriptiv statistikk – altså det å beskrive og oppsummere data – utgjør bare en bitteliten del av statistikken. Selv om deskriptiv statistikk er kraftig nok, så er de de virkelig kraftfulle sidene av statistikk de som gir deg mulighet til å trekke slutninger som går forbi dataene dine. Det er her statistikken virkelig viser sitt potensial!

Samme dag som jeg skriver dette rapporterer media om en ny meningsmåling der 28% av 1000 respondenter svarer at, om det hadde vært valg i dag, så hadde de stemt på Arbeiderpartiet. Dette viser at Arbeiderpartiet ligger an til å gjøre et godt valg, fortelles det. Ser du at dette går forbi deskriptiv statistikk? At 280 av 1000 personer svarte at de ville stemme Arbeiderpartiet betyr ikke at de vil gjøre et godt valg, for Arbeiderpartiet trenger mange flere stemmer enn 280 for å gjøre det godt. Det media gjør her er å tenke at disse 1000 personene sier noe om de 99,98% andre stemmeberettigede i Norge (ca. 4 350 000 personer) også.

Siden utvalget er tilfeldig, lærte vi i Seksjon 3.6.2 at utvalget i snitt blir representativt, men at man kan ha uflaks slik at akkurat utvalget du har trukket ikke er så representativt. Men hvor stort avvik kan man forvente? Bør man være overrasket om Arbeiderpartiet fikk \pm 5% av stemmene (altså 23% til 33%) om et annet meningsmålingsbyrå gjorde en tilsvarende undersøkelse samme dag? Hva med \pm 3%?

Inferensiell statistikk gir oss verktøyene vi trenger for å svare på slike spørsmål, og siden denne typen spørsmål står sentralt i mye vitenskapelig virksomhet, utgjør de størstedelen av de fleste innføringsbøker i kvantitativ metode, men ikke av denne boka. For det første er ikke dette nyttig når lærerstudenter skal skrive masteroppgave. Jeg har til dags dato ikke sett en masteroppgave som benytter tilfeldig utvalg eller tilfeldig gruppeinndeling, noe som er en forutsetning for å benytte de metodene som gis i innføringskurs i statistikk. For det andre har ikke lærerstudenter de matematiske forutsetningene for å forstå metodene, og, hvis jeg skal være ærlig, så er det få kvantitative forskere som forstå dem (se for eksempel McShane & Gal, 2015) og få lærebøker som introduserer dem riktig (se Cassidy et al., 2019). Vi er bedre tjent med å kun gi en kort innføring, slik at man kan lese og forstå litt av kvantitativ forskningslitteratur.

Teorien om statistisk inferens bygger på sannsynlighetsteori, så det må vi introdusere først. Denne gjennomgangen av sannsynlighetsteori er i hovedsak bakgrunnsstoff. Det er ikke så mye statistikk i seg selv i dette kapittelet, og du trenger ikke å forstå dette materialet like grundig som de andre kapitlene hvis du kun ønsker å gjøre utregningene. Men hvis du ønsker å forstå noe som helst, trenger du dette grunnlaget, spesielt å skjønne hva man mener med begrepene sannsynlighet og sannsynlighetsfordeling og hva normalfordelingen er.

6.1 Hva er forskjellen på sannsynlighet og statistikk?

Før vi starter på sannsynlighetsteorien er det nyttig å stoppe opp og tenke over forholdet mellom sannsynlighet og statistikk, for selv om disse fagområdene er nært beslektet, er de langt fra det samme.

Sannsynlighetsteori er “læren om tilfeldigheter” -– en matematisk gren som forteller oss hvor ofte ulike hendelser vil inntreffe. Her er noen eksempler på spørsmål som kan besvares med sannsynlighetsteori:

• Hvor stor er sjansen for at en rettferdig mynt lander på mynt 10 ganger på rad?
• Hvis jeg kaster en sekssidet terning to ganger, hvor sannsynlig er det at jeg får to seksere?
• Hvor sannsynlig er det å få kun hjerter hvis jeg trekker 5 kort fra en tilfeldig stokket kortstokk?
• Hvor stor er sjansen for at jeg vinner i lotto?

Legg merke hva alle disse spørsmålene har felles: vi vet hvordan verden oppfører seg, hvordan sannsynlighetene oppstår, hvilken mekanisme det er som genererer sannsynlighetene og hvordan den virker; og spørsmålet handler bare om hvilke hendelser som vil skje. I det første eksemplet vet jeg at mynten er rettferdig (50% sjanse for mynt på hvert kast). I det andre vet jeg at sjansen for å få 6 på en enkelt terning er 1 av 6. I det tredje vet jeg at kortstokken er ordentlig stokket, og i det fjerde vet jeg at lotteriet følger spesifikke regler. Det avgjørende poenget er at sannsynlighetsspørsmål starter med en kjent modell av verden, og vi bruker denne modellen til å gjøre beregninger. Modellen kan være ganske enkel. For myntkast-eksemplet kan vi skrive: P(\text{mynt}) = 0,5 som du kan lese som “sannsynligheten for mynt er 0,5”. (P står for probability.) Akkurat som prosenter varierer fra 0% til 100%, varierer sannsynligheter fra 0 til 1.

Når jeg bruker denne sannsynlighetsmodellen til å besvare spørsmål, vet jeg ikke nøyaktig hva som vil skje. Kanskje får jeg 10 mynt som spurt om, eller kanskje får jeg bare tre. Det er kjernen: I sannsynlighetsteori er modellen kjent, men dataene er ukjente.

Hva med statistikk? Statistiske spørsmål fungerer motsatt. I statistikk kjenner vi ikke sannheten om verden. Alt vi har er dataene, og fra disse ønsker vi å lære om verdens sanne natur. Statistiske spørsmål ser typisk slik ut:

• Hvis vennen min kaster en mynt 10 ganger og får mynt hver gang, lurer de meg?
• Hvis fem kort fra toppen av kortstokken alle er hjerter, hvor sannsynlig er det at kortstokken ble stokket ordentlig?
• Hvis lottosjefens ektefelle vinner i lotto, hvor sannsynlig er det at lotteriet var rigget?

Denne gangen har vi bare dataene. Jeg vet at vennen min kastet mynten 10 ganger og den landet på mynt hver gang. Jeg ønsker å konkludere om jeg skal tro at dette faktisk var en rettferdig mynt kastet 10 ganger på rad, eller om jeg burde mistenke juks. Dataene mine ser slik ut:

M M M M M M M M M M

Målet mitt er å finne ut hvilken “modell av verden” jeg bør stole på. Hvis mynten er rettferdig, bør modellen si at sannsynligheten for mynt er 0,5: P(mynt) = 0,5. Hvis mynten ikke er rettferdig, bør jeg konkludere med at P(mynt) ≠ 0,5.

Med andre ord: Det statistiske problemet handler om å finne ut hvilken sannsynlighetsmodell som er riktig basert på observerte data. Statistiske og sannsynlighetsmessige spørsmål er tydelig forskjellige, men henger tett sammen. Derfor begynner en god innføring i statistisk teori med en diskusjon av hva sannsynlighet er og hvordan det fungerer.

Eksempelet med mynt og kron er ikke så fjernt fra utdanningsforskning som du skulle tro. Se for deg at 10% av elevene ble kategorisert til å ha for dårlig lesekompetanse på forrige PISA-prøve, og nå er andelen 13%; i dette tilfellet har vi dataene, men vi lurer på om sannsynlighetsmodellen har forandret seg: trekker vi nå fra en populasjon med høyere andel på svakeste lesenivå enn ved forrige PISA-prøve?

6.2 Hva betyr sannsynlighet?

Hva er sannsynlighet? Det kan virke overraskende, men selv om statistikere og matematikere er enige om hva reglene for sannsynlighetsregning er, er det langt mindre enighet om hva ordet egentlig betyr. Det virker rart fordi vi alle er så vant med å bruke ord som “sjanse”, “sannsynlig”, “mulig” og “trolig”, så det burde da ikke være så vanskelig å si hva sannsynlighet er. Men tenk over følgende eksempel.

La oss anta at jeg vil tippe på en fotballkamp mellom to fotballlag, Rosenborg og Brann. Etter å ha tenkt en stund, bestemmer jeg meg for at det er 80% sannsynlighet for at Rosenborg vinner. Hva mener jeg med det? Her er tre muligheter:

• Hvis de kunne spille samme kamp om og om igjen, ville Rosenborg vinne 8 av hver 10 kamper i gjennomsnitt.
• Jeg er enig i at det å satse på denne kampen bare er “rettferdig” hvis en innsats på 4 kroner på Brann gir 5 kroner gevinst hvis de vinner, og at å satse 1 krone på Rosenborg gir 5 kroner.
• Min subjektive “tro” eller “tillit” til at Rosenborg vinner er fire ganger så sterk som min tro på Brann vinner, altså 80% mot 20%.

Hver av disse virker fornuftige, men de er ikke identiske og gir forskjellig svar på mange statistiske spørsmål. I denne boken kommer vi kun til å presentere den første definisjonen av sannsynlighet, som kalles frekventisme, fordi dette er en den i vanligst bruk, selv om den tredje definisjonen, Bayesianisme, ses oftere og oftere i noen deler av utdanningsforskningen.

6.2.1 Det frekventistiske synet på sannsynlighet

Den vanligste tilnærmingen til sannsynlighet kalles frekventisme og definerer sannsynlighet som en langsiktig frekvens. La oss si at vi kaster en rettferdig mynt om og om igjen og lurer på hva sjansen er for å få kron. Per definisjon er dette en mynt som har P(K) = 0,5. Hva ville vi observere? En mulighet er at de første 20 kastene kunne se slik ut:

M,K,K,K,K,M,M,K,K,K,K,M,K,K,M,M,M,M,M,K

I dette tilfellet kom 11 av disse 20 myntkastene (55%) opp som kron. La oss si at jeg fører en løpende oversikt over antall kron (som jeg kaller N_K) som jeg har sett gjennom de første N kastene, og beregner andelen kron \frac{N_K}{N} hver gang. Tabell 6.1 viser hva jeg fikk. (Jeg kastet faktisk en mynt for å lage dette!)

Tabell 6.1. Myntkast og andel kron

Antall kast	Antall kron	Andel kron
1	0	0.00
2	1	0.50
3	2	0.67
4	3	0.75
5	4	0.80
6	4	0.67
7	4	0.57
8	5	0.63
9	6	0.67
10	7	0.70
11	8	0.73
12	8	0.67
13	9	0.69
14	10	0.71
15	10	0.67
16	10	0.63
17	10	0.59
18	10	0.56
19	10	0.53
20	11	0.55

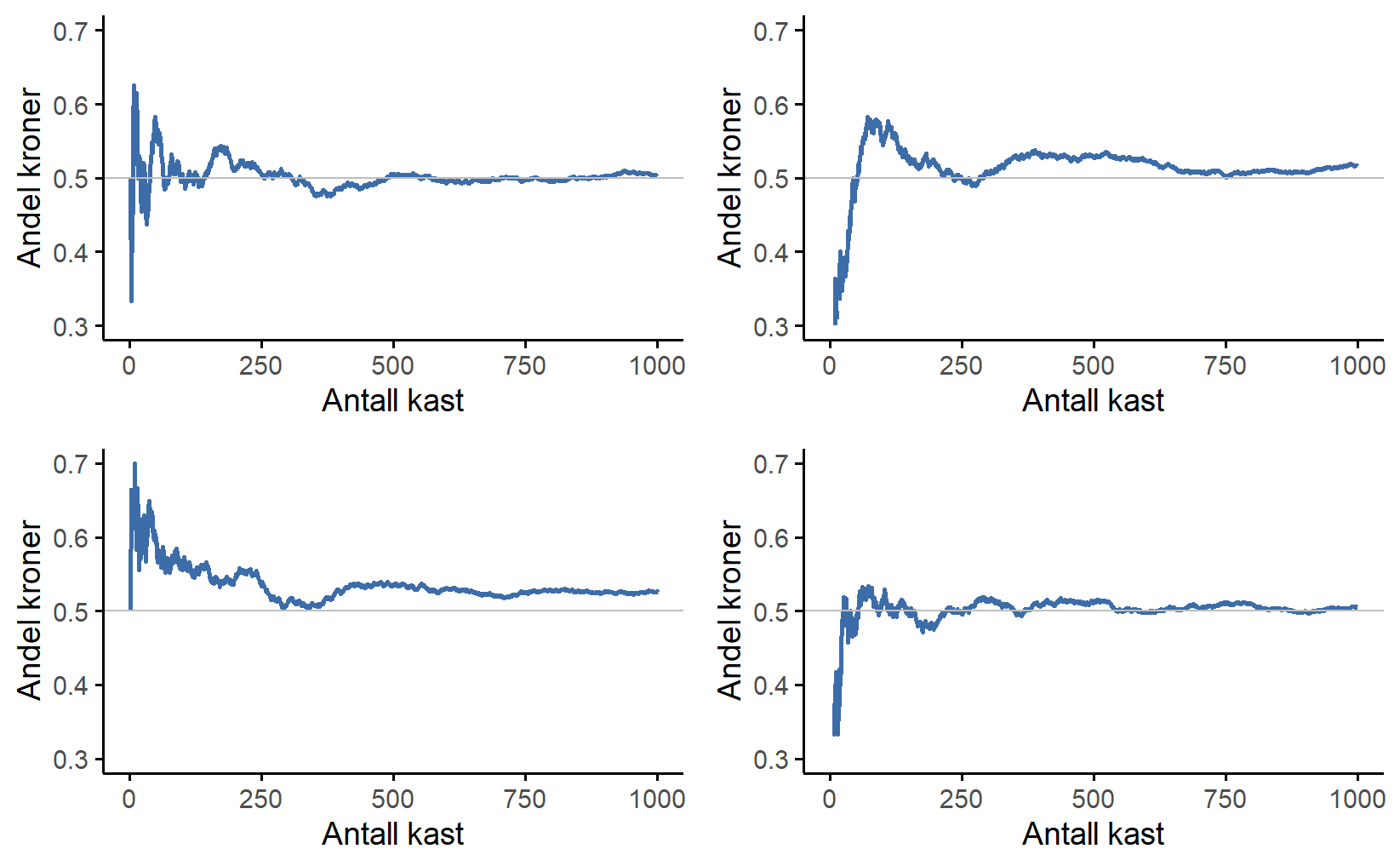
Legg merke til at i begynnelsen av sekvensen svinger andelen kroner vilt – den starter på 0,00 og stiger så høyt som 0,80. Senere ser det ut til at den roer seg ned, med flere og flere verdier som faktisk er ganske nær det “riktige” svaret på 0,50. Dette er den frekventistiske definisjonen av sannsynlighet i et nøtteskall: Sannsynligheten for kron er 50% hvis det å kaste en mynt om og om igjen i det uendelige, betegnet N \rightarrow \infty), vil andelen kron konvergere mot, altså nærme seg mer og mer, 50%. Det finnes noen subtile tekniske detaljer som matematikerne bryr seg om, men grovt sett er det slik frekventister definerer sannsynlighet.

Dessverre har jeg ikke et uendelig antall mynter eller den uendelige tålmodigheten som kreves for å kaste en mynt et uendelig antall ganger. Men jeg har en datamaskin, og datamaskiner er utmerkede til tankeløse repetitive oppgaver. Så jeg ba datamaskinen min simulere å kaste en mynt 1000 ganger og tegnet deretter et bilde av hva som skjer med andelen \frac{N_K}{N} når N øker. Faktisk gjorde jeg det fire ganger bare for å være sikker på at resultatet ikke var en tilfeldighet. Resultatene vises i Figur 6.1. Som du kan se, slutter andelen observerte kroner til slutt å svinge og roer seg ned. Når det skjer, er tallet den til slutt slår seg til ro på den sanne sannsynligheten for kron.

Figur 6.1. En illustrasjon av hvordan frekventistisk sannsynlighet fungerer. Hvis du kaster en rettferdig mynt om og om igjen, vil andelen kroner du har sett til slutt stabilisere seg og konvergere mot den sanne sannsynligheten på 0,5. Hvert panel viser fire forskjellige simulerte eksperimenter. I hvert tilfelle later vi som om vi kastet en mynt 1000 ganger og holdt oversikt over andelen kast som var kroner underveis. Selv om ingen av disse sekvensene faktisk endte opp med en eksakt verdi på 0,5, ville de ha gjort det hvis vi hadde utvidet eksperimentet til et uendelig antall myntkast

Den frekventistiske definisjonen av sannsynlighet har noen gode egenskaper. For det første er den objektiv: Sannsynligheten for en hendelse er forankret i en sekvens av hendelser, ikke i noens tro om hvor sannsynlig utfallene er. For det andre er den utvetydig: To personer som ser på den samme sekvensen av hendelser utfolde seg, og prøver å beregne sannsynligheten for en hendelse, må uunngåelig komme frem til det samme svaret. Den har imidlertid også uønskede egenskaper. Uendelige sekvenser eksisterer ikke egentlig i den fysiske verden. Man kan spørre seg om det gir mening å late som om en uendelig sekvens av myntkast eksisterer, for mynten vil jo bli slitt ned før man kommer så langt.

En mer alvorlig uønsket egenskap ved den frekventistiske definisjonen er at den har et snevert omfang. Det er mange ting der ute som mennesker tildeler sannsynlighet til i dagligspråket, men som ikke kan (selv i teorien) formuleres som en hypotetisk sekvens av hendelser. For eksempel, hvis en meteorolog kommer på TV og sier “sannsynligheten for regn i Oslo kommende onsdag er 60%”, aksepterer vi dette. Men det er ikke klart hvorfor dette er en sannsynlighet. Det er bare én by Oslo og bare én kommende onsdag. Det er ingen uendelig sekvens av hendelser her, bare en engangshendelse.

Frekventistisk sannsynlighet forbyr oss fra å lage sannsynlighetsuttalelser om en enkelt hendelse. Fra det frekventistiske perspektivet vil det enten regne i morgen eller så vil det ikke. Det er ingen “sannsynlighet” som knytter seg til en enkelt ikke-repeterbar hendelse.

Nå må det sies at frekventister har noen triks for å komme seg rundt dette. En mulighet er at det meteorologen mener er noe sånt som “Det finnes en kategori dager og steder som jeg predikerer 60% sjanse for regn for, og hvis vi bare ser på de dagene og stedene som jeg lager denne prediksjonen for, så vil det faktisk regne på 60% av de dagene og stedene. Kommende onsdag i Oslo er en slik dag og sted”. Det er veldig rart og kontraintuitivt å tenke på det på denne måten, men du ser frekventister gjøre dette noen ganger. Og det vil komme opp senere i denne boken (f.eks. i Seksjon 7.5).

6.3 Sannsynlighetsfordelinger

Selv om folk er rivende uenige i hva sannsynlighet er og hvordan sannsynligheter bør tolkes, så er folk stort sett enige om reglene som sannsynligheter følger. Vi skal ikke komme noe særlig inn på disse reglene, men reglene for sannynligheter er bakt inn i konseptet sannsynlighetsfordeling, og de må vi vite hva er.

Vi bruker buksene mine for å illustrere hva sannsynlighetsfordelinger er. Jeg eier fem par bukser og de har jeg gitt navnene X_1, X_2, X_3, X_4 og X_5. Hver dag velger jeg ut nøyaktig ett par bukser å ha på meg. Med sannsynlighetsteoriens språk, ville jeg omtalt hver bukse (dvs. hver X_i) som en elementær hendelse. En elementær hendelse er at hver gang vi gjør en observasjon (f.eks. hver gang jeg tar på meg et par bukser), så vil utfallet være én og bare én av disse hendelsene. Jeg har alltid på meg nøyaktig ett par bukser, så buksene mine tilfredsstiller denne begrensningen. På samme måte kalles mengden med alle mulige hendelser (altså X_1, X_2, ..., X_5) for et utfallsrom. Andre ville kanskje kalt det et “garderobeskap”.

OK, nå som vi vet at et utfallsrom er bygget opp av mange elementære hendelser ønsker vi å tildele en sannsynlighet til hver elementære hendelse. For en hendelse X_i er sannsynligheten for den hendelsen P(X_i) et tall som ligger mellom 0 og 1. Jo større verdien til P(X) er, desto mer sannsynlig er det at hendelsen inntreffer. For eksempel, hvis P(X) = 0 betyr det at hendelsen X er umulig (dvs. jeg har aldri på meg de buksene ¹ ). På den andre siden, hvis P(X) = 1 betyr det at hendelsen X er sikker (dvs. jeg har alltid på meg de buksene)². For sannsynlighetsverdier i midten betyr det at jeg noen ganger har på meg de buksene. For eksempel, hvis P(X) = 0.5 betyr det at jeg har på meg de buksene halvparten av tiden.

Til sist har vi loven om total sannsynlighet, som sier at sannsynligheten til de elementære hendelsene må summere til 1, altså at det er sikkert at en av hendelsene inntreffer. Hver gang jeg tar på meg bukser, ender jeg faktisk opp med å ha på meg bukser. Når disse kravene er oppfylt har vi det som kalles en sannsynlighetsfordeling. For eksempel viser Tabell 6.2 oet eksempel på en sannsynlighetsfordeling. Hver av hendelsene har en sannsynlighet som ligger mellom 0 og 1, og hvis vi adderer sannsynligheten for alle hendelsene summerer de seg til 1. Flott. Vi kan til og med tegne et fint stolpediagram (se Seksjon 5.1) for å visualisere denne fordelingen, som vist i Figur 6.2.

Tabell 6.2. En sannsynlighetsfordeling for buksebruk

Figur 6.2. En visuell fremstilling av “bukse”-sannsynlighetsfordelingen. Det er fem “elementære hendelser”, som tilsvarer de fem parene bukser jeg eier. Hver hendelse har en viss sannsynlighet for å inntreffe – denne sannsynligheten er et tall mellom 0 og 1. Summen av disse sannsynlighetene er 1

Og på dette punktet har vi alle oppnådd noe. Du har lært hva en sannsynlighetsfordeling er, og jeg har endelig klart å finne en måte å lage en graf som fokuserer utelukkende på buksene mine. Alle vinner! Det eneste andre jeg trenger å påpeke er at sannsynlighetsteori lar deg snakke om ikke-elementære hendelser i tillegg til elementære hendelser. Den enkleste måten å illustrere konseptet på er med et eksempel. I bukseeksemplet er det helt legitimt å referere til sannsynligheten for at jeg har på meg jeans. I dette scenariet sies hendelsen “Roar har på seg jeans” å ha skjedd så lenge den elementære hendelsen som faktisk inntraff er en av de passende. I dette tilfellet “blå jeans”, “sorte jeans” eller “grå jeans”. I matematiske termer definerte vi “jeans”-hendelsen E til å tilsvare mengden med elementære hendelser (X1, X2, X3). Hvis noen av disse elementære hendelsene inntreffer, sies også E å ha inntruffet. Etter å ha bestemt oss for å skrive ned definisjonen av E på denne måten, er det ganske enkelt å oppgi hva sannsynligheten P(E) er: vi adderer bare alt sammen. I dette tilfellet, siden sannsynlighetene for henholdsvis blå, grå og sorte jeans er 0,5, 0,3 og 0,1, er sannsynligheten for at jeg har på meg jeans lik 0,9: P(E)=P(X_1)+P(X_2)+P(X_3)

Du tenker kanskje at dette er helt åpenbart og enkelt, og det er kanskje rett. Alt vi egentlig har gjort er å pakke inn sunn fornuft i litt grunnleggende matematikk. Imidlertid bygger noen kraftige verktøy på disse enkle definisjonene. Jeg kommer definitivt ikke til å gå inn i detaljene i denne boken, men vi må komme oss til en kontinuerlig sannsynlighetsfordeling som heter normalfordelingen, og da må vi starte med binomisk fordeling.

6.4 Noen vanlige sannsynlighetsfordelinger

Som du kan tenke deg, varierer sannsynlighetsfordelinger enormt. Men de er ikke alle like viktige. Denne boken bygger på fem fordelinger: binomisk fordeling, normalfordeling, t-fordeling, \chi^2-(“kjikvadrat”)-fordeling og F-fordeling. Vi skal ikke lære noe om alle fem, men for å vise hva de går ut på og hvorfor normalfordelingen er så, vel, normal, skal jeg beskrive binomisk fordeling og hvordan den leder til normalfordelingen.

6.4.1 Binomialfordelingen

Sannsynlighetsteorien oppstod i forsøket på å finne de beste strategiene i gambling-spill med terning eller kortstokk, så det er passende at vi diskuterer binomialfordelingen med terningkast. En binomialfordeling er sannsynlighetsfordelingen man får når man gjør et tilfeldig forsøk med to utfall (suksess og ikke suksses) mange ganger og teller opp antall suksesser man har fått. Man kaller sannsynligheten for suksess for for \theta og antall ganger man gjør forsøket for N.

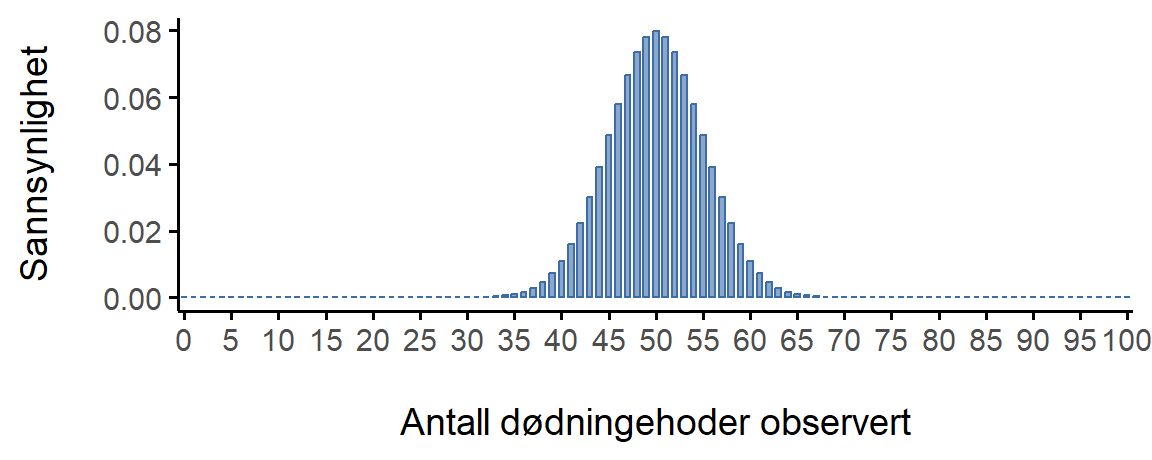
I vårt terningeksempel holder jeg 20 identiske sekssidede terninger. På den ene siden av hver terning er det et bilde av et dødninghode, de resterende fem sidene er hvite. Hvis jeg kaster alle 20 terningene, hva er sannsynligheten for at jeg får nøyaktig 4 dødninghoder? I utdanningsforskning kan dette tilsvare noe slikt: Hvis en av seks elever er på høyeste nivå lesing i 8. trinn og du trekker 20 elever tilfeldig, hva er sannsynligheten for at 4 av dem er på høyeste nivå? Dette høres oppkonstruert ut, men husk at sannsynlighetsregning er en forutsetning for inferensiell statistikk, og det statistiske spørsmålet kunne lydt: “Fire av 20 elever i utvalget er på høyeste nivå i lesing. Hvilken andel i populasjonen er på høyeste nivå i lesing?”

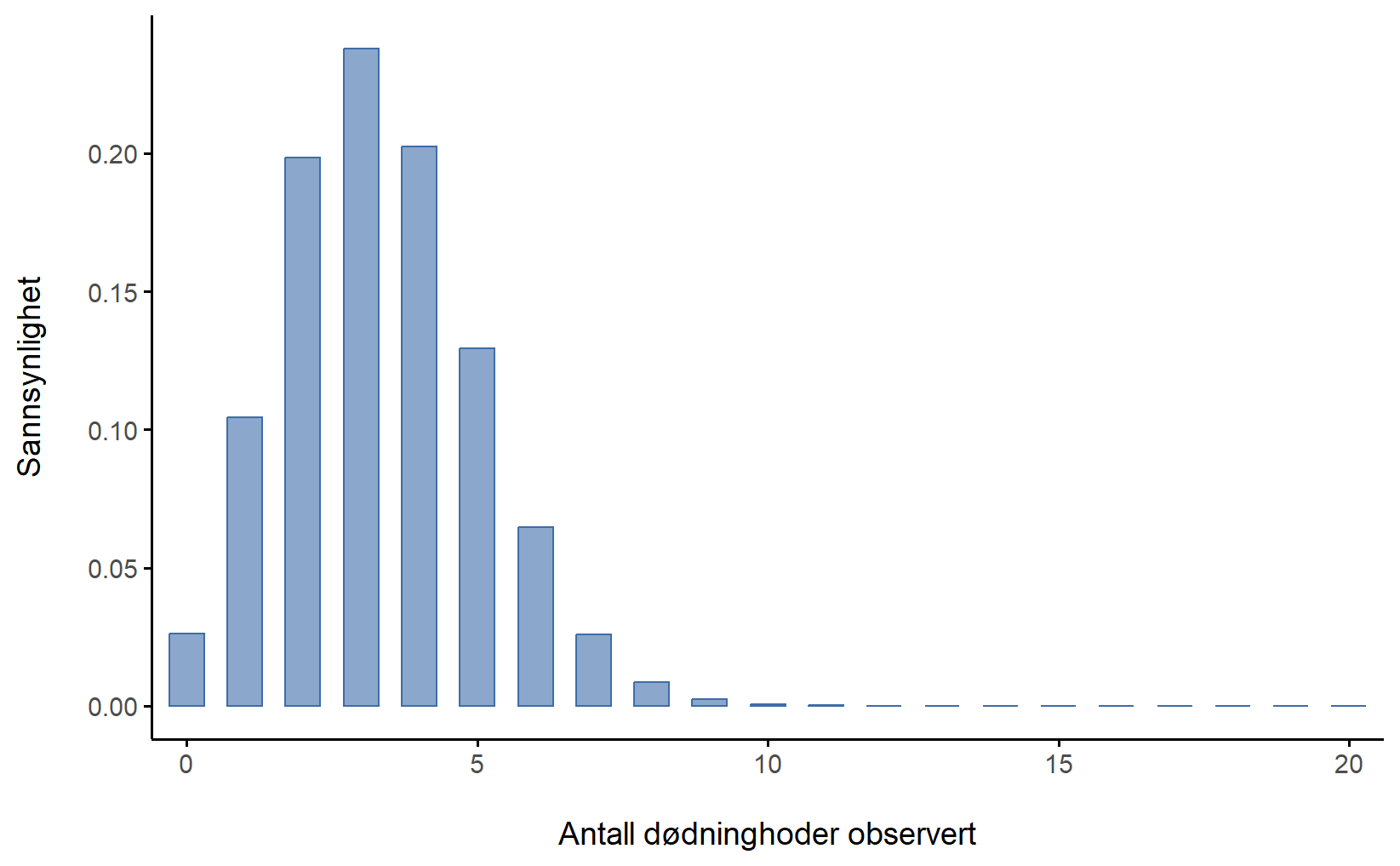
Terningforsøket følger en binomisk sannsynlighetsfordeling siden det er 20 identiske forsøk, to hendelser (dødninghode og ikke dødninghode) og vi lurer på antall suksesser. Siden sjansen for dødninghode er 1 av 6, har vi \theta = \frac{1}{6} = 0.167. Siden det er 20 forsøk har vi N = 20. vet vi noe som tilsvarer 0,167. Dette er nok informasjon til å finne den binomiske fordelingen, som er vist i Figur 6.3.

Figur 6.3 viser den binomiske sannsynlighetsfordelingen for alle mulige verdier av X for vårt terningkast-eksperiment, fra X = 0 (ingen dødninghoder) helt opp til X = 20 (alle dødninghoder). Merk at dette i bunn og grunn er et stolpediagram, og er ikke forskjellig fra “bukse-sannsynlighets”-plottet jeg tegnet i Figur 6.2. På den horisontale aksen har vi alle de mulige hendelsene, og på den vertikale aksen kan vi lese av sannsynligheten for hver av disse hendelsene. Så sannsynligheten for å få 4 dødninghoder av 20 er omtrent 0,20 (det faktiske svaret er 0,2022036). Med andre ord kan du forvente at det skjer omtrent 20% av gangene du gjentar dette eksperimentet.

Figur 6.3. Binomialfordelingen med N = 20 og sannsynlighet for suksess på \theta = \frac{1}{6}. Hver vertikale stolpe viser sannsynligheten for ett spesifikt utfall (dvs. én mulig verdi av X). Fordi dette er en sannsynlighetsfordeling, må hver av sannsynlighetene være et tall mellom 0 og 1 og høydene på stolpene må summere til 1

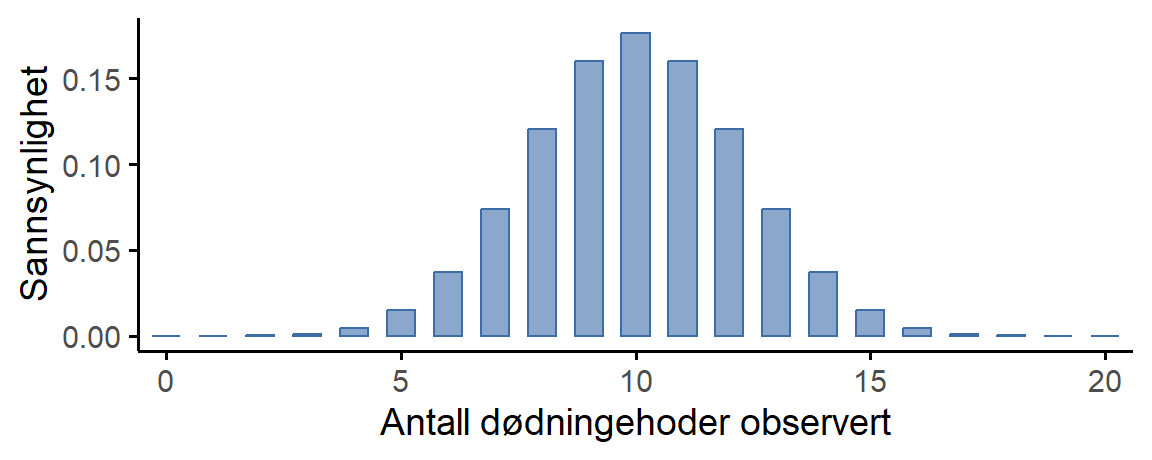
For å gi deg en følelse av hvordan binomialfordelingen endrer seg når vi endrer verdiene til \theta og N, la oss anta at i stedet for å kaste terninger, kaster jeg faktisk mynter. Denne gangen involverer eksperimentet mitt å kaste en rettferdig mynt gjentatte ganger, og utfallet jeg er interessert i er antall kron jeg observerer. I dette scenariet er suksess-sannsynligheten nå \theta = \frac{1}{2}. Anta at jeg skulle kaste mynten N = 20 ganger. I dette eksemplet har jeg endret suksess-sannsynligheten men beholdt størrelsen på eksperimentet. Hva gjør dette med binomialfordelingen vår? Som Figur 6.4 (a) viser, er hovedeffekten av dette å forskyve hele fordelingen, akkurat som du ville forvente.

Greit, hva hvis vi kastet en mynt N = 100 ganger? I så fall får vi Figur 6.4 (b). Fordelingen holder seg omtrent i midten, men det er litt mer variasjon i de mulige utfallene.

(a) Kast av mynten N = 20 ganger.

(b) Kast av mynten N = 100 ganger.

Figur 6.4. To binomialfordelinger hvor jeg kaster en rettferdig mynt (\theta = \frac{1}{2}) med forskjellig verdi for N.

Fordelingene i disse figurene ser kanskje kjente ut, og det er nok fordi de likner på normalfordelingen, og med større N hadde de bare blitt likere og likere normalfordelingen.

6.4.2 Normalfordelingen

Selv om binomialfordelingen er den enkleste fordelingen å forstå, er den ikke den viktigste. Den spesielle æren tilhører normalfordelingen, også omtalt som “the bell curve”, siden den likner litt på en bjelle, eller en “Gausskurve”, etter Carl Friedrich Gauss, som utledet fordelingen for å beskrive feilene i astronomiske observasjoner. En normalfordeling beskrives ved hjelp av to parametere: gjennomsnittet til fordelingen \mu, “my”, og standardavviket til fordelingen \sigma, “sigma”. ³ Notasjonen som vi noen ganger bruker for å si at en variabel X er normalfordelt er som følger: X \sim Normal(\mu,\sigma)

La oss opparbeide en følelse for hva det betyr at en variabel er normalfordelt. Ta en titt på Figur 6.5 som viser en normalfordeling med gjennomsnitt \mu = 0 og standardavvik \sigma = 1. (Akkurat denne normalfordelingen kalles en standard normalfordeling.)

Figur 6.5. Normalfordelingen med gjennomsnitt \mu = 0 og standardavvik \sigma = 1. På x-aksen vil man typisk finne verdien til en variabel, og y-aksen forteller hvor sannsynlig det er at vi observerer den verdien.

Legg merke til at i motsetning til figurene jeg tegnet for å illustrere binomialfordelingen, viser bildet av normalfordelingen i Figur 6.5 en jevn kurve i stedet for “histogram-lignende” søyler. Dette er fordi normalfordelingen er kontinuerlig mens binomialfordelingen ikke er det. For eksempel, i terningkast-eksemplet fra forrige seksjon var det mulig å få 3 kron eller 4 kron, men umulig å få 3,9 kron. Figurene jeg tegnet i forrige delkapittel reflekterte dette. I Figur 6.3, for eksempel, er det en søyle plassert ved X = 3 og en annen ved X = 4, men det er ingenting imellom. Kontinuerlige fordelinger har ikke denne begrensningen. I praksis er normalfordelingen så praktisk at folk har en tendens til å bruke den selv når variabelen faktisk ikke er kontinuerlig. Så lenge det er nok kategorier (f.eks. en 5-punkts Likert-spørsmål på et spørreskjema), er det ganske standard praksis å bruke normalfordelingen som en tilnærming. Dette fungerer mye bedre enn du skulle tro.

Note

Det er et subtilt og noe frustrerende kjennetegn ved kontinuerlige fordelinger som gjør at y-aksen oppfører seg litt merkelig – høyden på kurven her er faktisk ikke sannsynligheten for å observere en bestemt x-verdi. Men det er sant at høydene på kurven forteller deg hvilke x-verdier som er mer sannsynlige (de høyere!). y-verdiene viser en “sannsynlighetstetthet”, som du kan lese om et annet sted, hvis du er interessert.

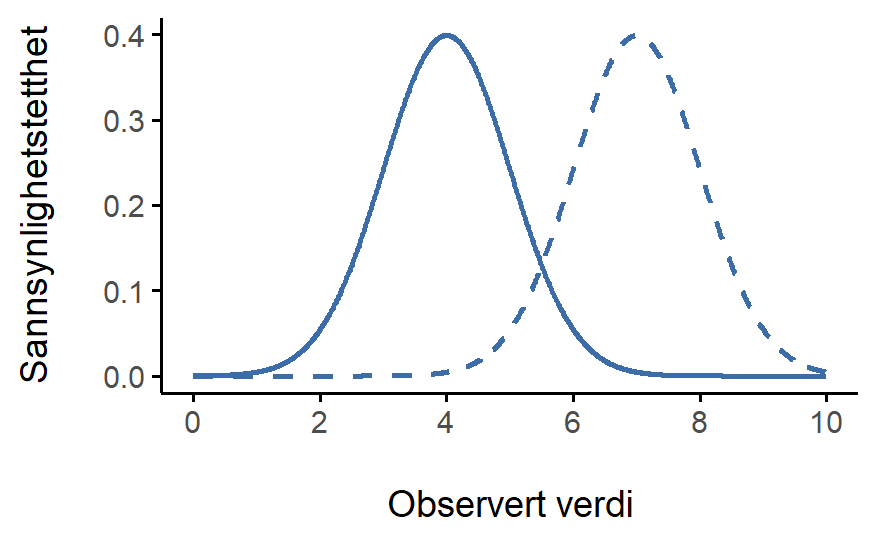
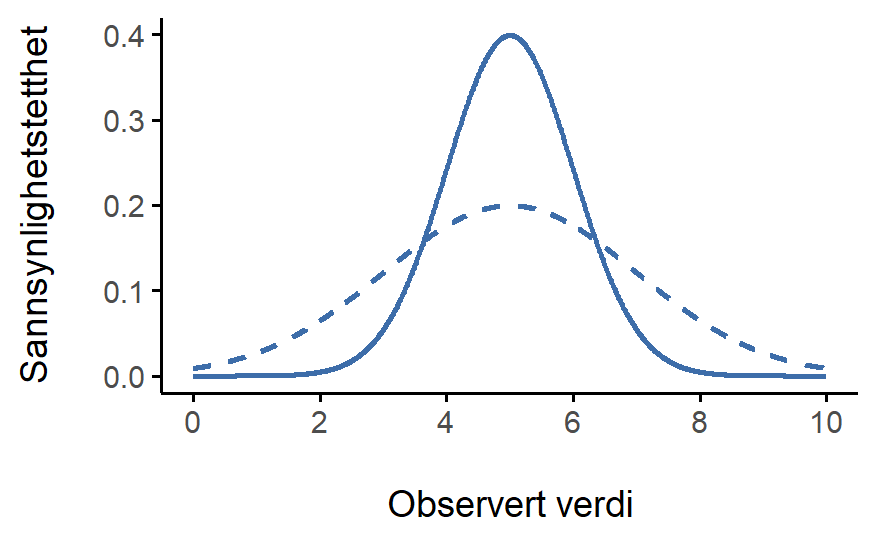
La oss nå se om vi kan få en intuisjon for hvordan normalfordelingen fungerer. Først ser vi hva som skjer når vi leker med parametrene til fordelingen. Figur 6.6 viser derfor normalfordelinger som har forskjellige gjennomsnitt, men samme standardavvik. Alle disse fordelingene samme “bredde”. Den eneste forskjellen mellom dem er at de har blitt forskjøvet til venstre eller høyre. På alle andrem åter er de identiske. Derimot, hvis vi øker standardavviket mens vi holder gjennomsnittet konstant, forblir fordelingen sentrert på samme sted, men fordelingen blir bredere, som du kan se i Figur 6.7. Legg merke til at når vi utvider fordelingen, synker høyden på toppen. Dette må skje, for på samme måte som høydene på søylene vi brukte til å tegne en diskret binomialfordeling må summere til 1, må det totale arealet under kurven for normalfordelingen være lik 1.

Figur 6.6. En illustrasjon av hva som skjer når du endrer gjennomsnittet til en normalfordeling. Den heltrukne linjen viser en normalfordeling med gjennomsnitt \mu = 4. Den stiplede linjen viser en normalfordeling med gjennomsnitt \mu = 7. I begge tilfeller er standardavviket \sigma = 1. Ikke overraskende har de to fordelingene samme form, men den stiplede linjen er forskjøvet til høyre

Figur 6.7. En illustrasjon av hva som skjer når du endrer standardavviket til en normalfordeling. Begge fordelingene som er plottet i denne figuren har gjennomsnitt \mu = 5, men de har forskjellige standardavvik. Den heltrukne linjen viser en fordeling med standardavvik \sigma = 1, og den stiplede linjen viser en fordeling med standardavvik \sigma = 2. Som en konsekvens er begge fordelingene “sentrert” på samme sted, men den stiplede linjen er bredere enn den heltrukne

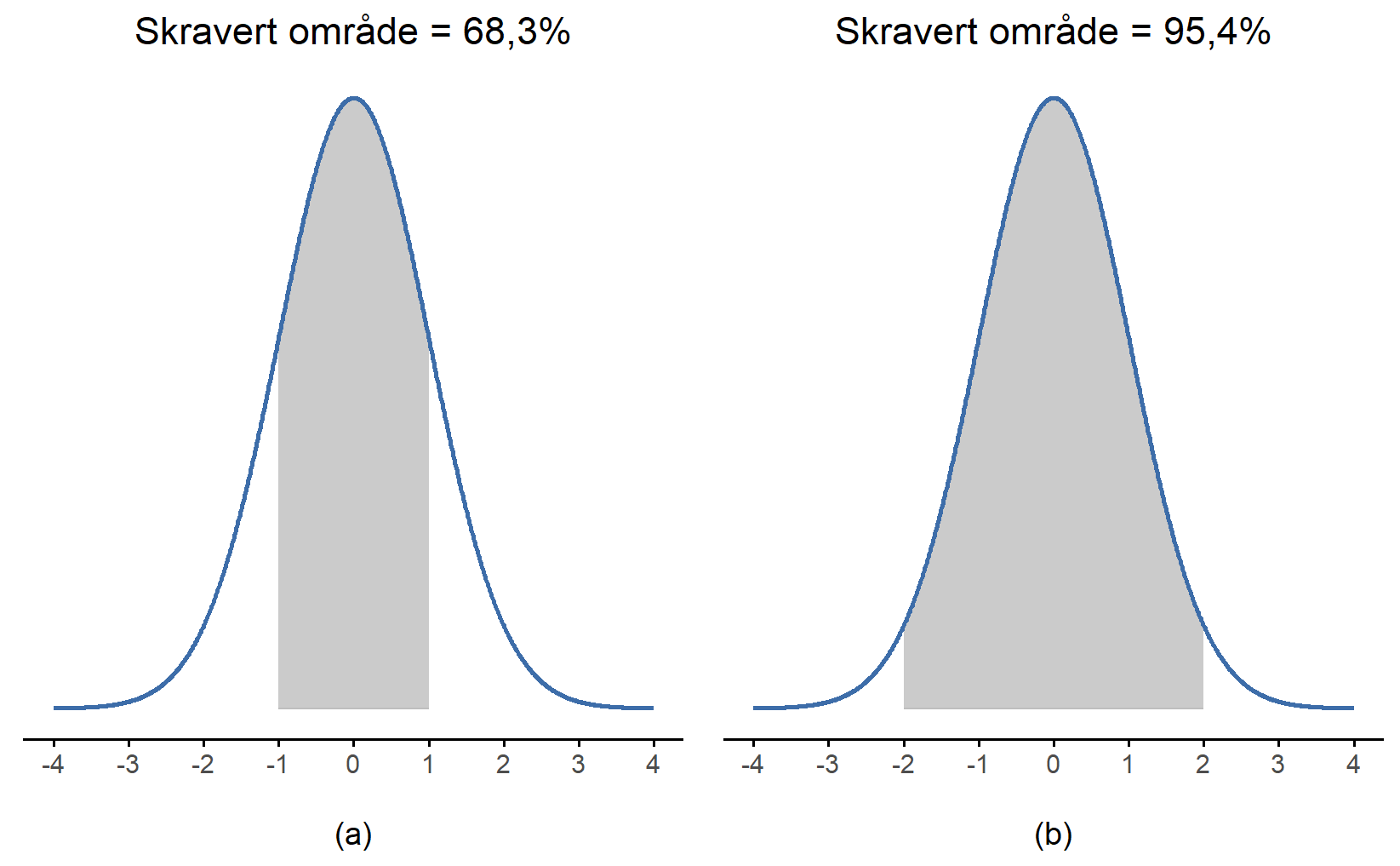
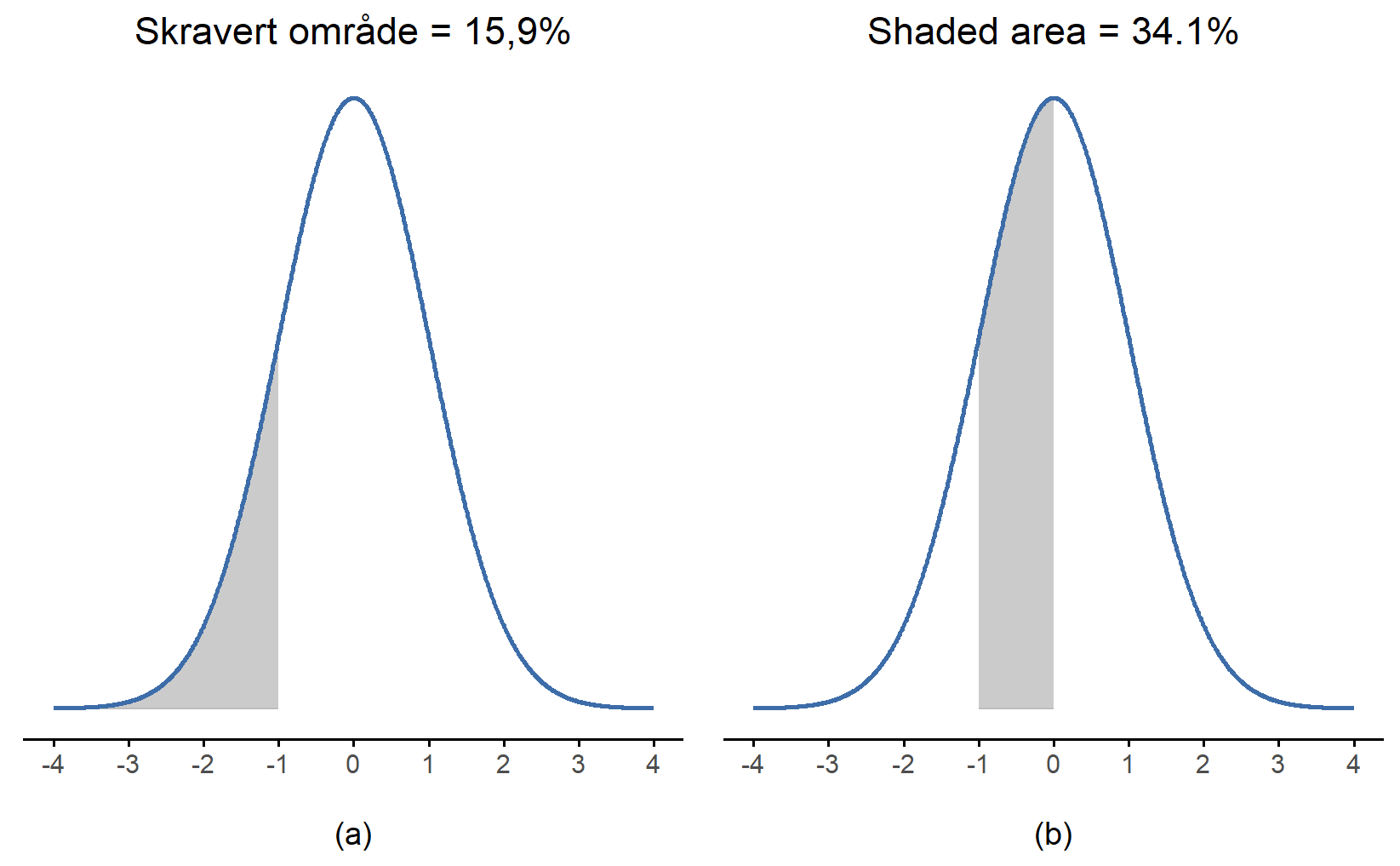
Uansett hvilke verdier gjennomsnittet og standardavviket har, vil alltid nøyaktig 68.3\% av arealet under kurven befinne seg innenfor 1 standardavvik fra gjennomsnittet, 95.4\% av fordelingen finner vi innenfor 2 standardavvik fra gjennomsnittet, og hele 99.7\% ligger innenfor 3 standardavvik. Denne regelen, som vi nevte i Seksjon 4.4.4 og som ofte kalles “68-95-99.7-regelen”, er illustrert i Figur 6.8. For en enda mer detaljert forklaring kan du også ta en titt på Figur 6.9.

Figur 6.8. Arealet under kurven forteller deg sannsynligheten for at en observasjon faller innenfor et bestemt område. De heltrukne linjene viser normalfordelinger med gjennomsnitt \mu = 0 og standardavvik \sigma = 1. De skraverte områdene illustrerer “areal under kurven” for to viktige tilfeller. I panel (a) kan vi se at det er 68,3% sjanse for at en observasjon vil falle innenfor ett standardavvik fra gjennomsnittet. I panel (b) ser vi at det er 95,4% sjanse for at en observasjon vil falle innenfor to standardavvik fra gjennomsnittet

Figur 6.9. To eksempler til på “arealet under kurven”-ideen. Det er 15,9% sjanse for at en observasjon er ett standardavvik under gjennomsnittet eller mindre (panel (a)), og 34,1% sjanse for at observasjonen er et sted mellom ett standardavvik under gjennomsnittet og gjennomsnittet (panel (b)). Legg merke til at hvis du legger disse to tallene sammen får du 15,9% + 34,1% = 50%. For normalfordelte data er det 50% sjanse for at en observasjon faller under gjennomsnittet. Og det innebærer selvfølgelig også at det er 50% sjanse for at den faller over gjennomsnittet

6.4.3 De andre sannsynlighetsfordelingene vi trenger

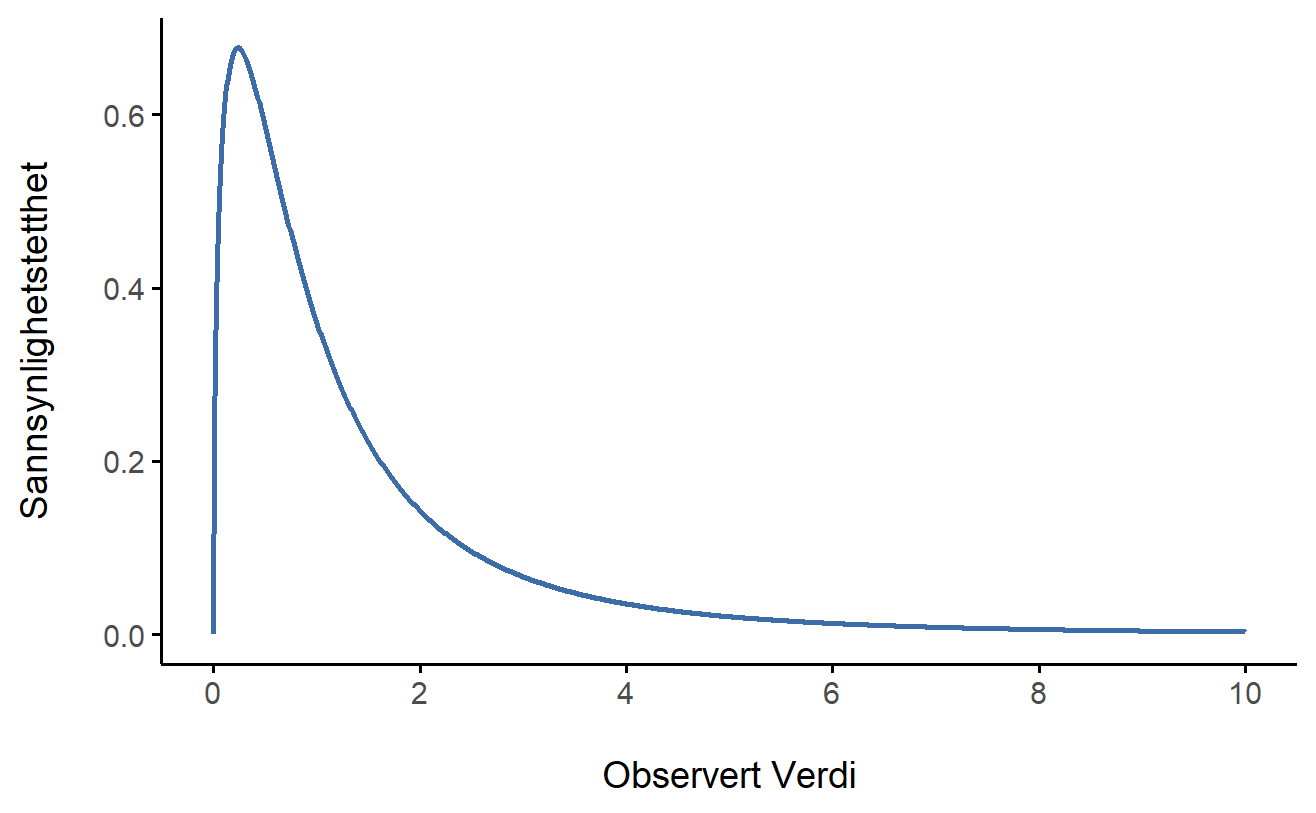
Normalfordelingen er den mest brukte fordelingen i statistikk (vi skal snart se hvorfor), og binomialfordelingen er svært nyttig for mange formål. Men statistikkens verden inneholder mange sannsynlighetsfordelinger, og vi vil møte to av dem, \chi^2-fordelingen (uttales “kji-kvadrat”) og F-fordelingen. Jeg vil ikke gå inn på formlene for disse, eller snakke om dem i stor detalj, men la oss se på hvordan de ser ut: Figur 6.10 og Figur 6.11.

Figur 6.10. \chi^2-fordeling med 3 frihetsgrader. Legg merke til at de observerte verdiene alltid må være større enn null, og at fordelingen er ganske skjev. Dette er nøkkelegenskapene til en kji-kvadrat-fordeling

Figur 6.11. En F-fordeling med 3 og 5 frihetsgrader. Kvalitativt sett ser den ganske lik ut som en kji-kvadrat-fordeling, men de er ikke helt like generelt sett

\chi^2-fordelingen dukker opp mange steder i statistikk. Vi vil se den når vi analyserer kategoriske variable i Kapitel 9, men den er faktisk svært vanlig. Matematisk sett oppstår \chi^2-fordelingen når vi har flere normalfordelte variabler, kvadrerer verdiene deres og legger dem sammen (en “sum av kvadrater”). Dette viser seg å være utrolig nyttig! Figur 6.10 viser hvordan en \chi^2-fordeling ser ut.

F-fordelingen ligner litt på \chi^2-fordelingen og brukes når vi skal sammenligne to \chi^2-fordelinger. Dette høres kanskje rart ut, men er faktisk svært viktig i dataanalyse. Siden \chi^2 er nøkkelfordelingen for “summer av kvadrater”, bruker vi F-fordelingen når vi vil sammenligne to forskjellige “summer av kvadrater”. Vi skal se eksempler på dette i Kapitel 10. Figur 6.11 viser hvordan F-fordelingen ser ut.

La oss oppsummere: Vi har nå møtt to nye fordelinger - \chi^2 og F. Disse er kontinuerlige fordelinger og er nært beslektet med normalfordelingen. Det viktigste å forstå er at disse fordelingene henger tett sammen med hverandre og med normalfordelingen. Senere i boken vil vi støte på data som er normalfordelt, eller som vi antar er normalfordelt. Når du gjør denne antagelsen, vil du ofte se \chi^2-, t- og F-fordelinger dukke opp naturlig i dataanalysen din.

6.5 Sammendrag

I dette kapittelet har vi gitt en kort oversikt over sannsynlighet som er nyttig i statistikk. Vi presenterte først hva sannsynlighet betyr for de fleste forskere, nemlig frekventisme, og hvorfor statistikere ikke alltid er enige om hva sannsynlighet er. Vi gikk gjennom de grunnleggende reglene som sannsynligheter må følge, og oppsummert dem i konseptet “sannsynlighetsfordeling”. I resten av kapittelet presenterte vi de viktigste sannsynlighetsfordelingene for vårt arbeid videre, \chi^2- og F-fordelingen. Her er en oversikt over hovedtemaene:

• Sannsynlighet versus statistikk: Hva er forskjellen på sannsynlighet og statistikk?
• Det frekventistiske synet på sannsynlighet.
• Sannsynlighetsfordelinger.
• Binomialfordelingen, Normalfordelingen, og De andre sannsynlighetsfordelingene vi trenger, \chi^2 og F.

Dette kapittelet kan virke som en omvei. Mange kurs i statistikk hopper over å diskutere det grunnleggende og går heller rett videre til hvordan man regner ut ting. Vi gjør det omvendt og inkluderer noe av grunnlaget til statistikken og hopper over hvordan man faktisk gjør utregningene. Utregningene er opplysende, men de krever mer tid enn man har i et kurs om kvantitativ metode for lærere, og da er det viktigere å kunne tenke konseptuelt og få en datamaskin til å faktisk gjøre utregningene.

Cassidy, S. A., Dimova, R., Giguère, B., Spence, J. R., & Stanley, D. J. (2019). Failing Grade: 89% of Introduction-to-Psychology Textbooks That Define or Explain Statistical Significance Do So Incorrectly. Advances in Methods and Practices in Psychological Science, 2515245919858072. https://doi.org/10.1177/2515245919858072

McShane, B. B., & Gal, D. (2015). Blinding Us to the Obvious? The Effect of Statistical Training on the Evaluation of Evidence. Management Science, 62(6), 1707–1718. https://doi.org/10.1287/mnsc.2015.2212

---

1. De som husker den frekventistiske definisjonen av sannsynlighet vil kanskje kverulere og si at det bare er andelen ganger X inntreffer som må gå mot null når N går mot uendelig, og at det derfor er mulig. De har rett.

2. Samme innvending gjelder her.

3. Hvis dere ønsker en føling med hvordan det matematiske uttrykket til normalfordelingen er, værsågod: p(X|\mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(X-\mu)^2}{2\sigma^2}} Wow, hva gjør \pi der?!