| variable | min | max | mean | median | std. dev | IQR |
|---|---|---|---|---|---|---|
| Danielles grettenhet | 41.00 | 91.00 | 63.71 | 62.00 | 10.05 | 14.00 |
| Danielles søvn (timer) | 4.84 | 9.00 | 6.97 | 7.03 | 1.02 | 1.45 |
| Babyens søvn (timer) | 3.25 | 12.07 | 8.05 | 7.95 | 2.07 | 3.21 |
11 Korrelasjon og lineær regresjon
Målet i dette kapittelet er å introdusere korrelasjon og lineær regresjon. Dette er standardverktøy som statistikere bruker når de analyserer sammenhengen mellom to kontinuerlige variable.
Heller ikke i dette kapittelet har jeg ikke rukket å gjøre eksemplene relevante for utdanningsvitenskap. Det er mye arbeid å finne relevante datasett fra utdanningsvitenskap og forklare analysene ved hjelp av dem, og det rakk jeg ikke før semesterstart for dette kapittelet. Derfor er eksempelet hentet fra originalboka Navarro & Foxcroft (2025), og er nok oppkonstruert.
11.1 Korrelasjon
Hvordan kan vi beskrive sammenhengen mellom ulike variabler i et datasett? En vanlig og effektiv metode er å se på korrelasjonen mellom dem. For å illustrere dette, trenger vi et datasett å jobbe med (Tabell 11.1).
11.1.1 Dataene
La oss ta for oss et tema småbarnsforeldre kjenner seg igjen i: søvn. Tenk deg at jeg, Danielle, er nysgjerrig på hvordan søvnmønsteret til spedbarnet mitt påvirker mitt eget humør. Jeg har derfor samlet inn data om min egen og babyen min sin søvn over 100 dager. Datasettet er fiktivt, men inspirert av ekte småbarnsliv. Jeg har vurdert min egen grettenhet på en skala fra 0 (blid som en sol) til 100 (ekstremt gretten) og i tillegg registrert hvor mange timer både jeg og babyen har sovet. Som den datanerden jeg er, har jeg lagret alt i en fil kalt parenthood.csv.
Når vi laster inn filen, ser vi at den inneholder fire variabler: dani.sleep, baby.sleep, dani.grump og day. Når du laster inn data i jamovi, er det lurt å sjekke at programmet har tolket datatypene riktig. I dette tilfellet bør dani.sleep, baby.sleep og dani.grump settes som kontinuerlige variabler, markert med et linjal-ikon i jamovi, mens ID-variabelen kan være nominell, markert med tre sirkler.
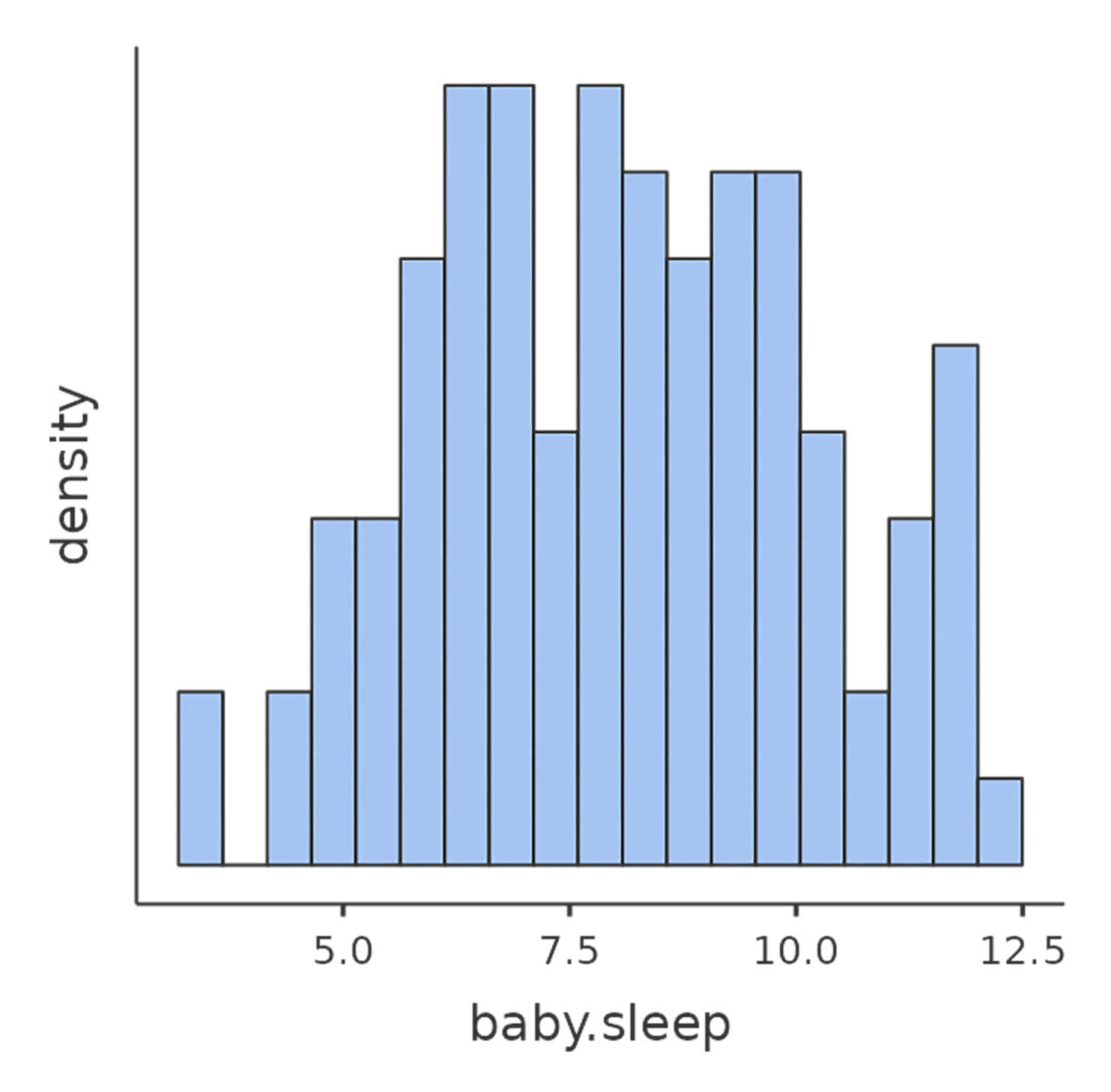
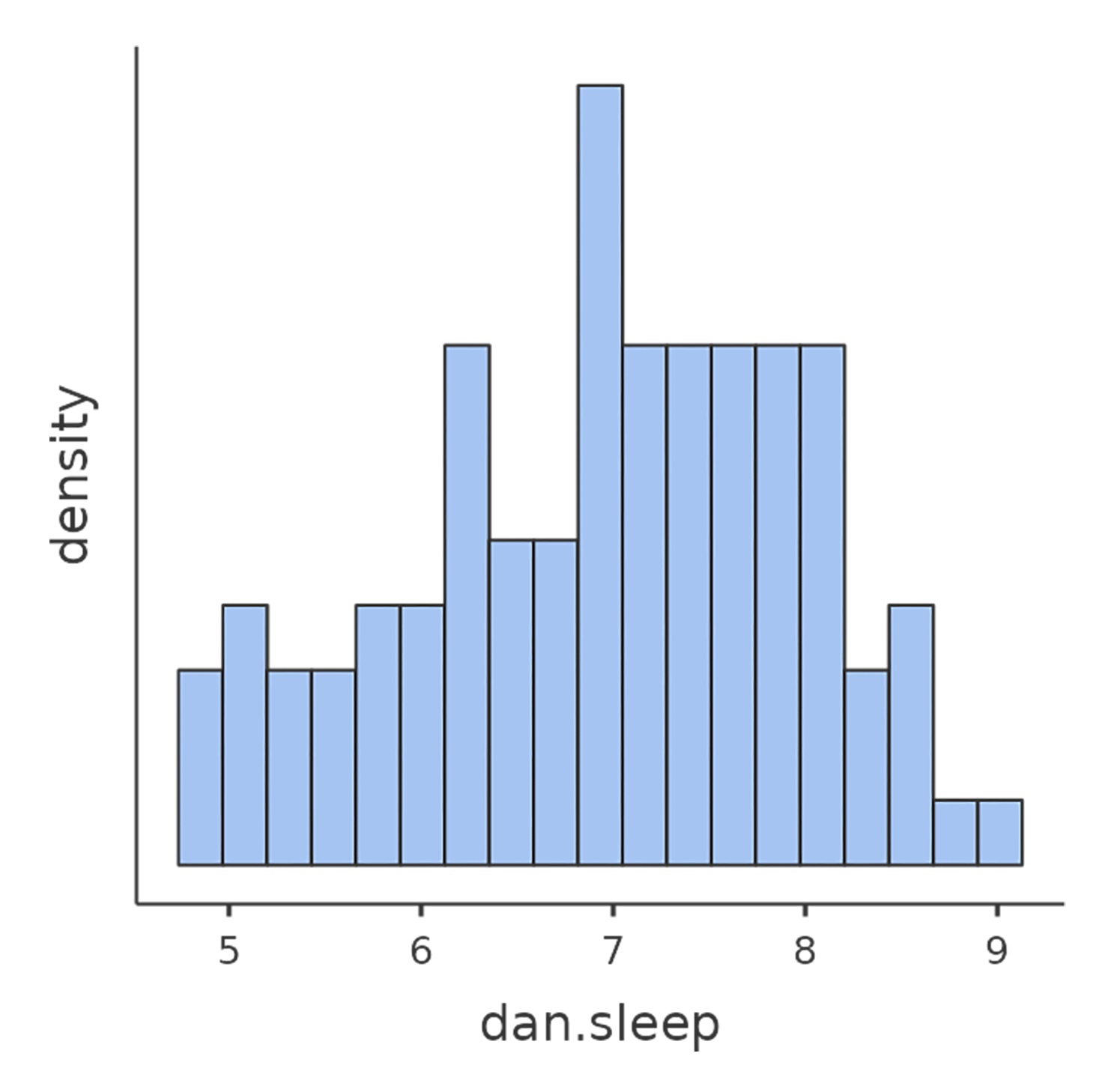
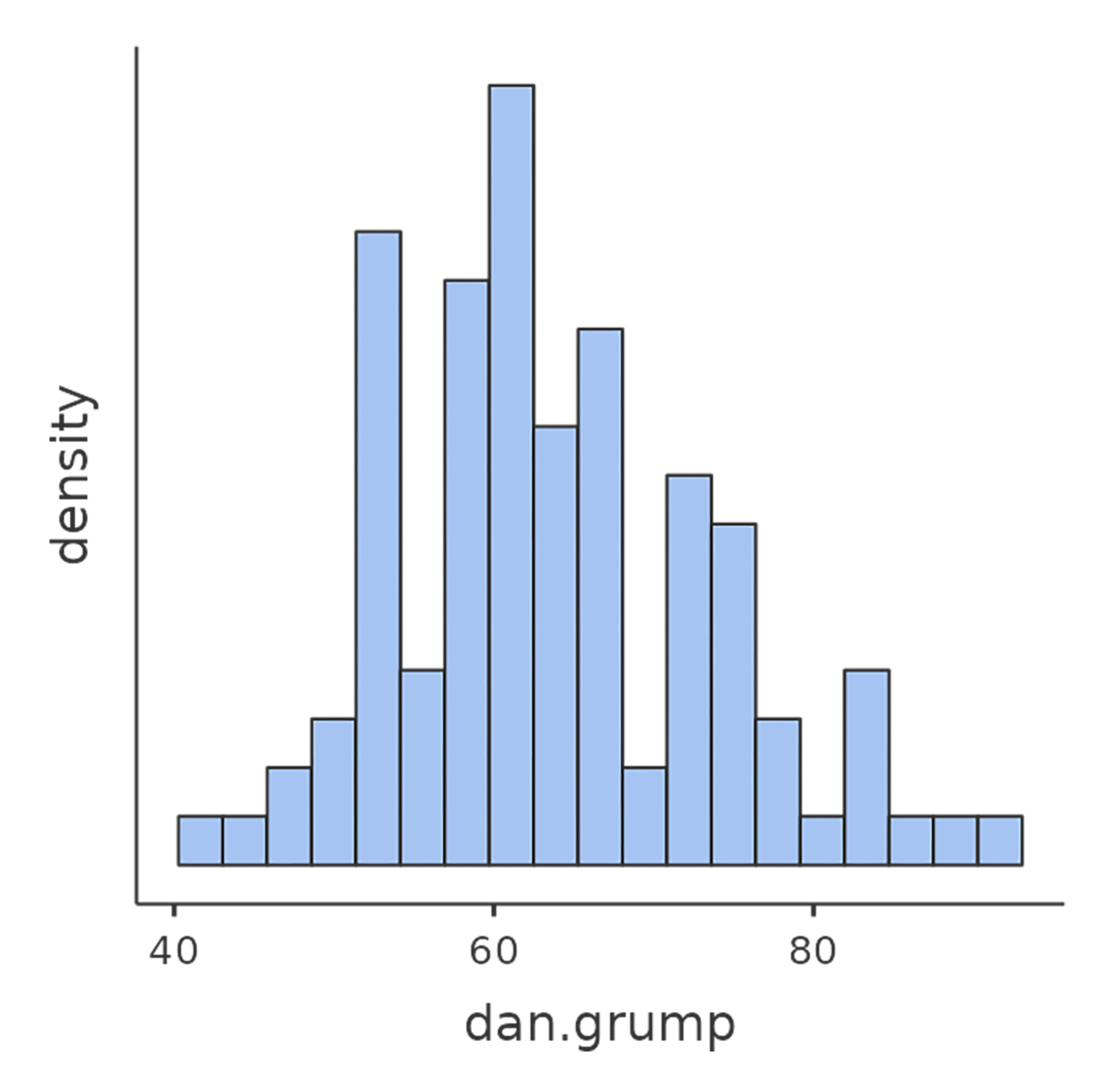
La oss starte med å se på deskriptiv statistikk og å visualisere variablene, siden det er god praksis. Figur 11.1 viser histogrammer for de tre mest interessante variablene, slik at vi får et visuelt inntrykk av fordelingen. Her er et godt råd: Selv om jamovi kan produsere en imponerende mengde statistikk uten at du trenger å gjøre noe som helst, bør du bare rapportere det som er relevant. I en rapport ville jeg valgt ut de viktigste tallene og presentert dem i en ryddig og lettlest tabell, slik som i Tabell 11.1.1 Legg merke til at jeg har gitt variablene «menneskevennlige» navn i tabellen – det er alltid lurt. Du vil kanskje også legge merke til at jeg ikke får nok søvn. Det er neppe god praksis, men andre småbarnsforeldre forsikrer meg om at det er helt normalt.
11.1.2 En korrelasjons styrke og retning
Et spredningsplott gir oss en god pekepinn på hvordan to variabler henger sammen, men ofte vil vi gjerne si noe mer presist enn bare å se på et bilde.
Ta en titt på de to plottene nedenfor. Det til venstre (Figur 11.2 (a)) viser sammenhengen mellom hvor mye babyen sover (baby.sleep) og hvor gretten jeg er (dani.grump). Det til høyre (Figur 11.2 (b)) viser sammenhengen mellom min egen søvn (dani.sleep) og grettenheten min. Når vi ser dem side om side, er det lett å se at begge forteller samme historie: mer søvn betyr mindre grettenhet! Men det er også tydelig at sammenhengen er mye sterkere i det høyre plottet. Punktene ligger tettere samlet, og plottet ser rett og slett mer «ryddig» ut. Det kjennes som om jeg kunne gjettet humøret mitt ganske greit om jeg visste hvor mye sønnen min hadde sovet, men jeg hadde truffet enda bedre om jeg visste hvor mye jeg hadde sovet selv.
baby.sleep og dani.grump (venstre) og sammenhengen mellom dani.sleep og dani.grump (høyre)
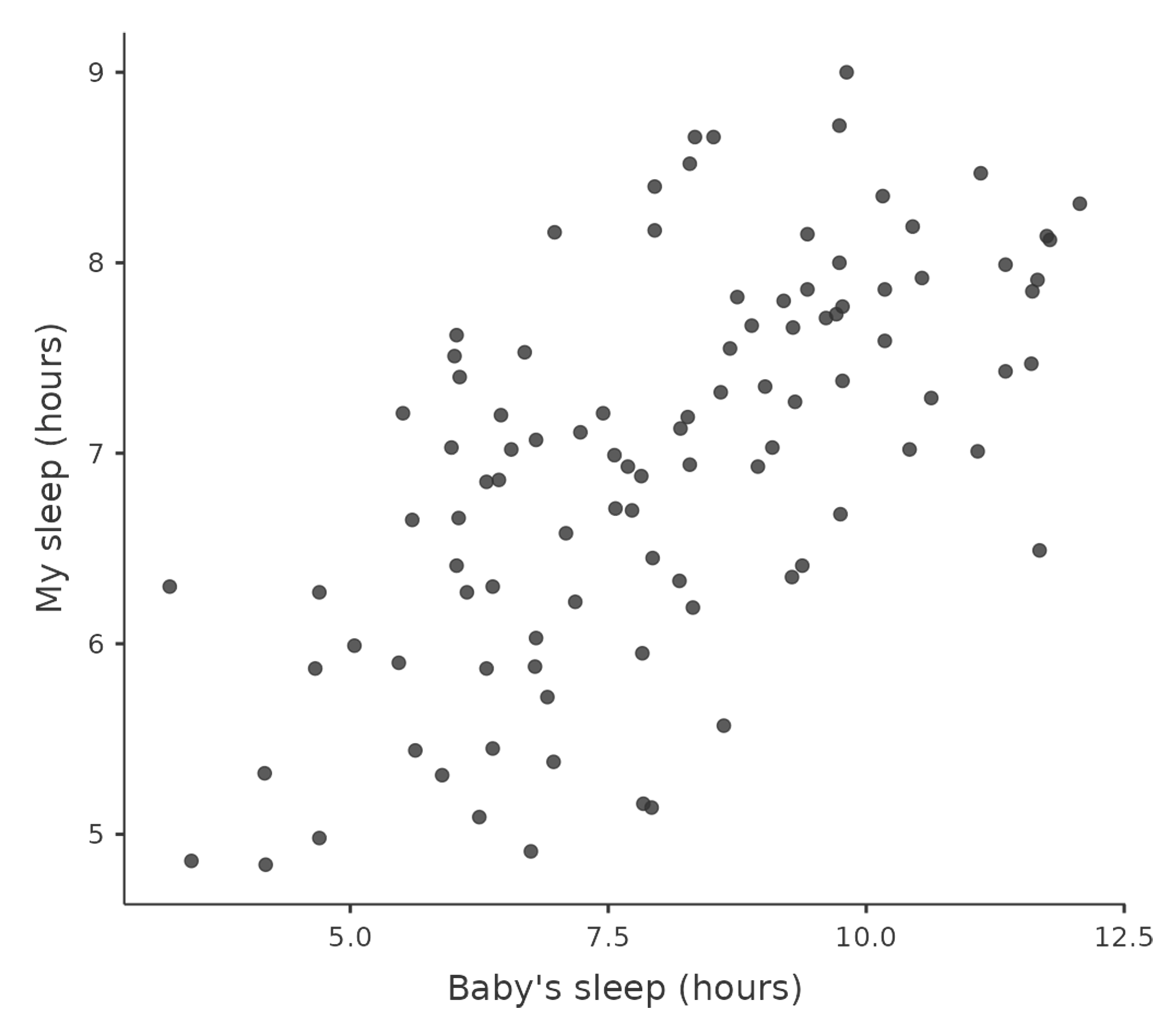
Nå som vi har sett på styrken i en sammenheng, la oss se på retningen. Ta en titt på de to plottene i figur Figur 11.3. Her sammenligner vi sammenhengen mellom babyens søvn og min grettenhet (til venstre) med sammenhengen mellom babyens søvn og min søvn (til høyre). Denne gangen er styrken i de to sammenhengene ganske lik, men retningen er helt motsatt. Det betyr at når sønnen min sover mer, får også jeg mer søvn – en positiv sammenheng (plottet til høyre). Samtidig, når han sover mer, blir jeg mindre gretten – en negativ sammenheng (plottet til venstre).
11.1.3 Korrelasjonskoeffisienten
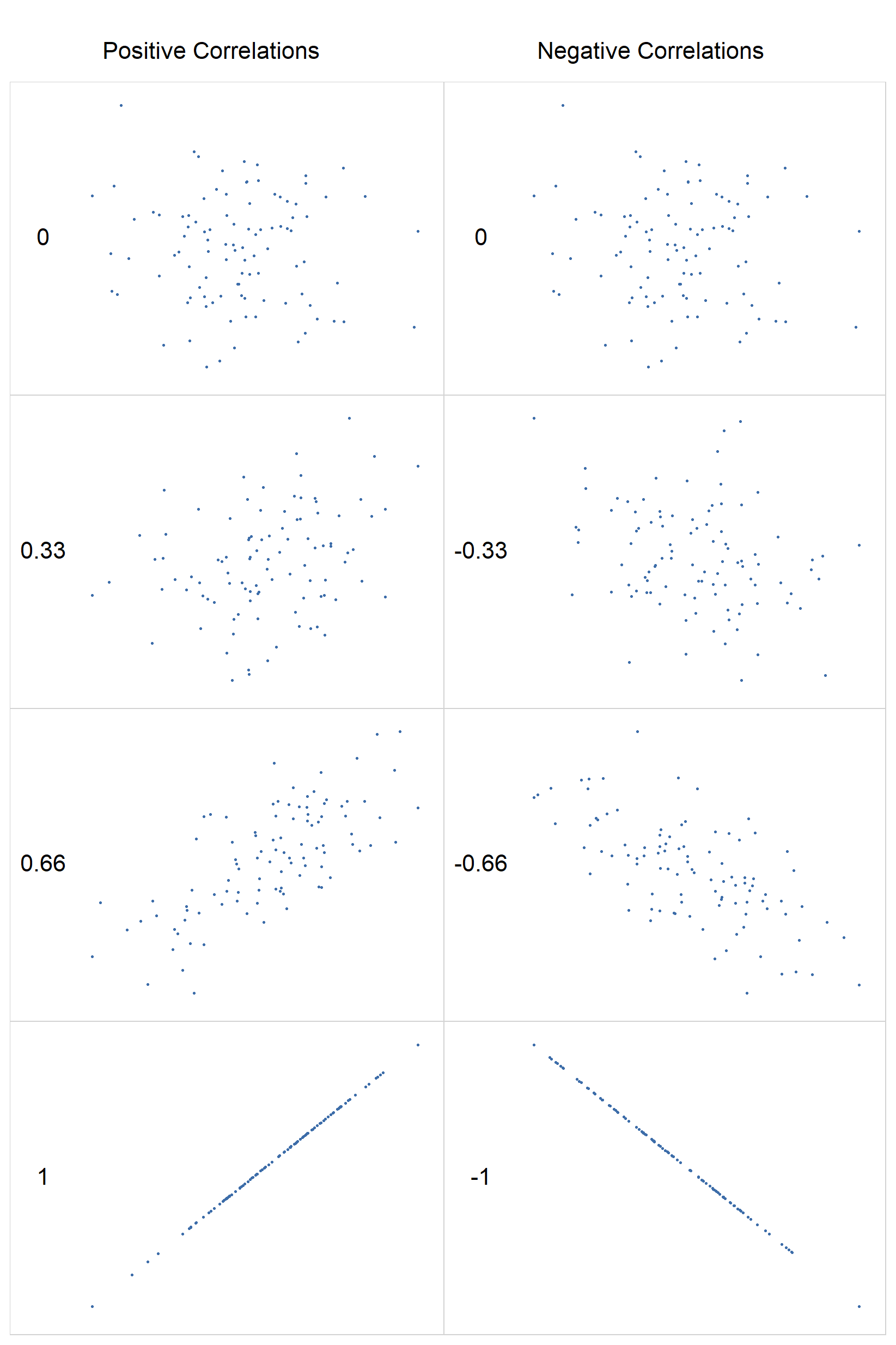
For å få et bedre grep om disse ideene, la oss introdusere korrelasjonskoeffisienten. Den kalles ofte Pearsons korrelasjonskoeffisient og skrives som r. Denne koeffisienten er et tall mellom -1 og 1 som måler styrken og retningen på sammenhengen mellom to variabler, X og Y (noen ganger skrevet r_{XY}).
- En r = 1 betyr en perfekt positiv sammenheng.
- En r = -1 betyr en perfekt negativ sammenheng.
- En r = 0 betyr at det ikke er noen lineær sammenheng i det hele tatt.
Ta en titt på figur Figur 11.4 for å se eksempler på hvordan ulike korrelasjoner ser ut.
Vi ser at korrelasjonen måler i hvor stor grad punktene faller på en rett linje i et spredningsplott. Dette er velegnet til å beskrive sammenhengen mellom kontinuerlige variable.
11.1.4 Beregne korrelasjoner i jamovi
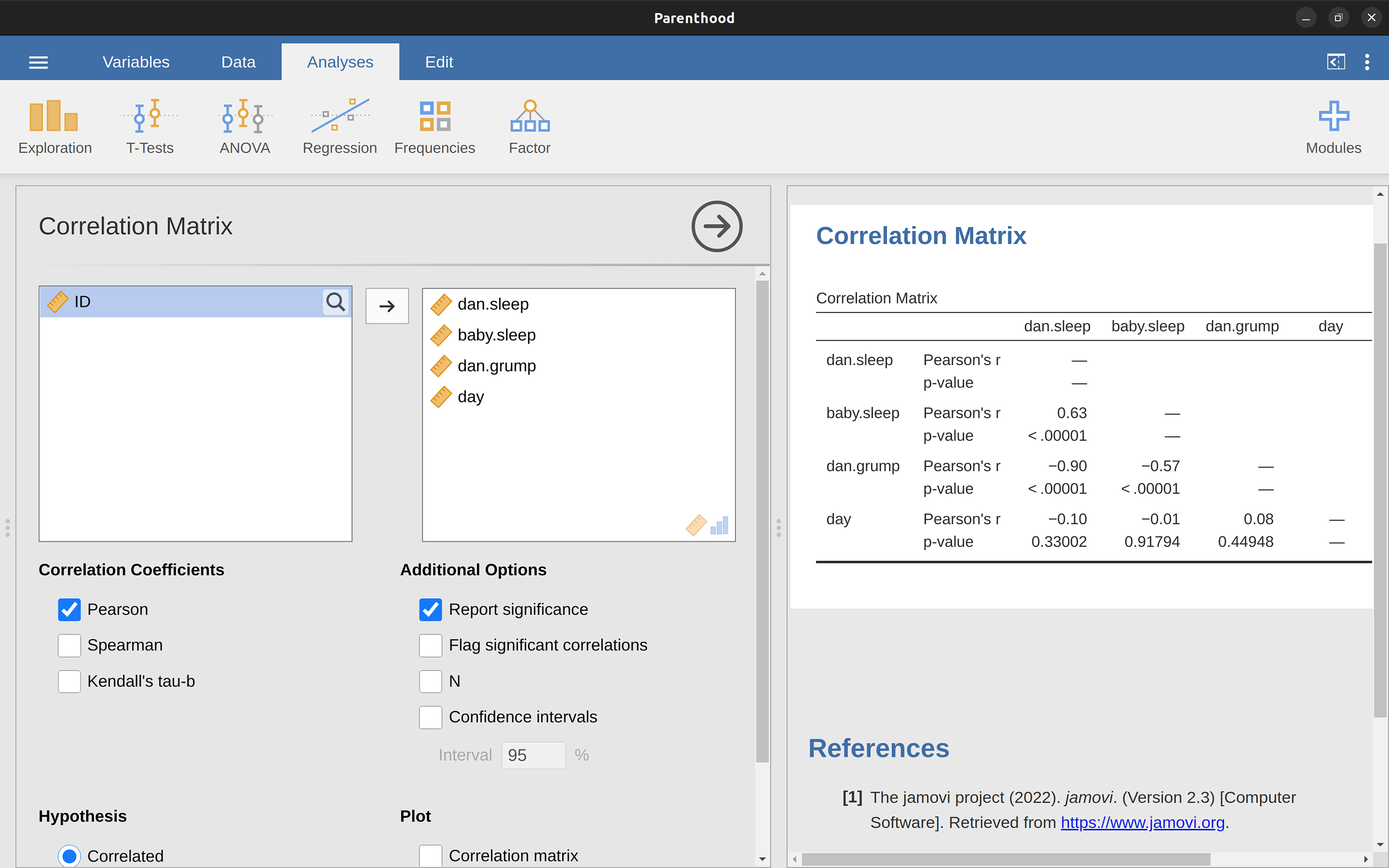
For å beregne korrelasjoner i jamovi, klikker du på ‘Regression’ → ‘Correlation Matrix’-knappen. Flytt alle fire kontinuerlige variablene over i boksen til høyre for å få resultatet vist i Figur 11.5.
11.1.5 Tolkning av en korrelasjon
I det virkelige liv ser man sjelden korrelasjoner på 1. Så hvordan skal man tolke en korrelasjon på, si, r = 0{,}4? Det ærlige svaret er at det avhenger av hva du skal bruke dataene til, og hvor sterke korrelasjonene i fagfeltet ditt pleier å være. En ingeniørvenn av meg argumenterte en gang for at enhver korrelasjon under 0{,}95 er helt ubrukelig (jeg tror han overdrev, selv for ingeniørfag). På den annen side finnes det reelle tilfeller, selv innen psykologi, hvor man bør forvente så sterke korrelasjoner. For eksempel er et av referansedatasettet som brukes til å teste teorier om hvordan folk bedømmer likheter så rent at studier som ikke oppnår en korrelasjon på minst 0{,}9 ikke anses som vellykket. Men når man ser etter, for eksempel, korrelasjoner mellom undervisning og læring gjør man det svært bra hvis man får en korrelasjon på 0{,}3. Men hvis man korrelerer hvor godt en elev gjør det på den samme rettskrivningprøven på mandag og på tirsdag, bør den vise svært høy korrelasjon. Kort sagt, tolkningen av en korrelasjon avhenger i stor grad av konteksten. Når det er sagt, er det mange som benytter veiledere som i Tabell 11.2. Tja, jo, hvorfor ikke.
| Korrelasjon | Styrke | Retning |
|---|---|---|
| Merk at dette er en grov veiledning. Det finnes ingen nøyaktige regler for hva som er en sterk og svake sammenheng. Det avhenger av konteksten. | ||
| -1,0 til -0,9 | Veldig sterk | Negativ |
| -0,9 til -0,7 | Sterk | Negativ |
| -0,7 til -0,4 | Moderat | Negativ |
| -0,4 til -0,2 | Svak | Negativ |
| -0,2 til 0 | Ubetydelig | Negativ |
| 0 til 0,2 | Ubetydelig | Positiv |
| 0,2 til 0,4 | Svak | Positiv |
| 0,4 til 0,7 | Moderat | Positiv |
| 0,7 til 0,9 | Sterk | Positiv |
| 0,9 til 1,0 | Veldig sterk | Positiv |
Vi kan ikke få sagt det nok: Se alltid på spredningsplottet før du begynner å tolke dataene. Grunnen er enkel: En korrelasjon betyr ikke alltid det du tror.
Et klassisk eksempel som viser dette perfekt, er «Anscombes kvartett» (Anscombe, 1973). Kvartetten består av fire datasett, og hvert av dem har en X- og en Y-variabel. Kvartetten er laget slik at de deskriptive statistikkene er så å si identiske for alle fire:
- Gjennomsnittet for alle X-variablene er 9{,}0 og for alle Y-variablene er 7{,}5.
- Standardavvikene er også praktisk talt like for både X og Y.
- Og for å toppe det hele, er korrelasjonen mellom X og Y i alle de fire tilfellene r = 0{,}816.
Dette kan du forresten enkelt sjekke selv, for dataene ligger klare i filen anscombe.csv.
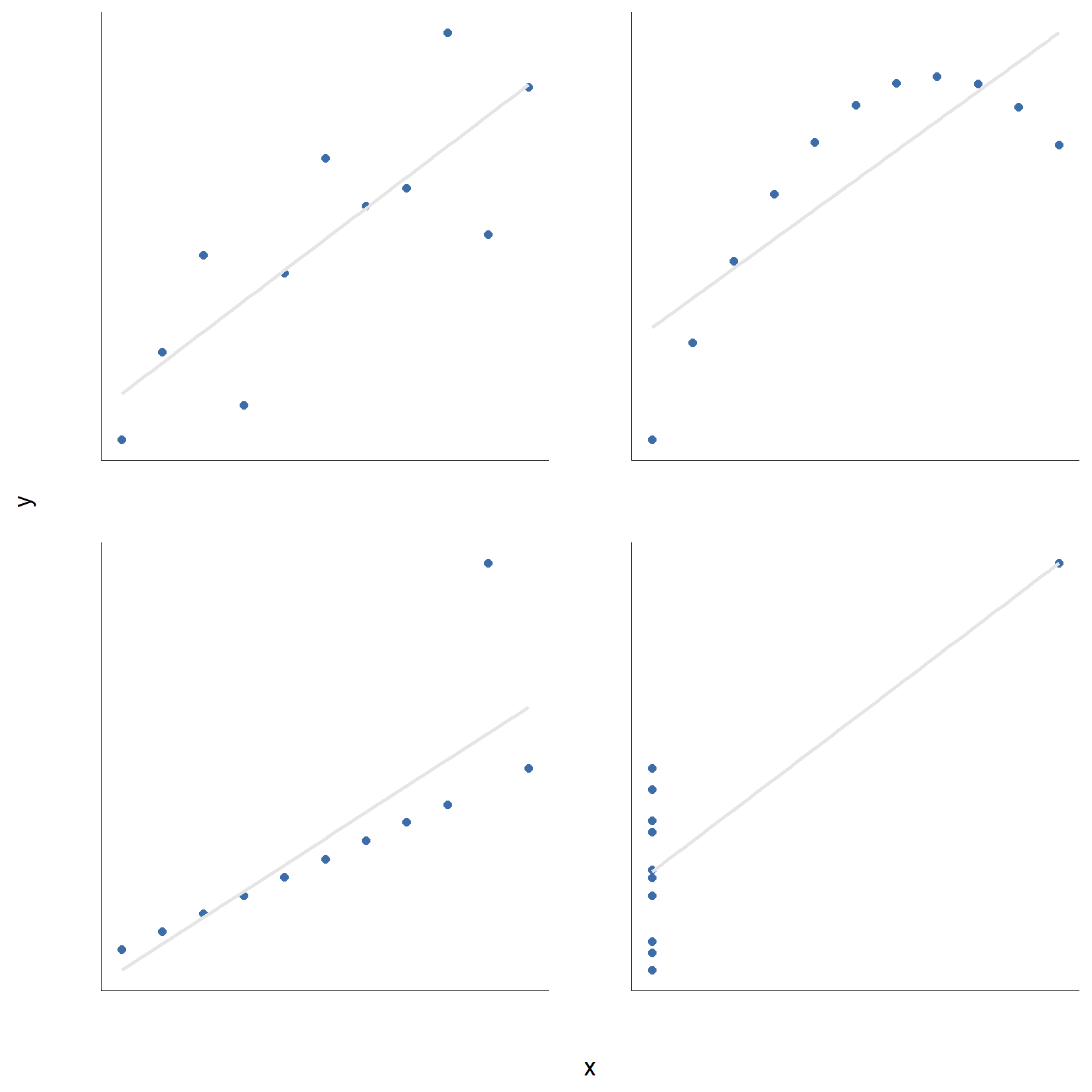
Basert på kun disse tallene skulle man tro at datasettene er nokså like, men det er de absolutt ikke. Først når vi visualiserer dataene som spredningsplott, slik du ser i Figur 11.6, avsløres sannheten: De fire datasettene er helt ulike. Da skjønner vi hvorfor mange statistikere har følgende leveregel, som mange dessverre glemmer i praksis:
Visualiser alltid dataene dine!
11.2 Lineær regresjon
Lineær regresjon kan ses på som en mer avansert og kraftfull versjon av Pearsons korrelasjon, som vi så på i forrige kapittel. For å se nærmere på dette, henter vi frem igjen datasettet parenthood.csv. Husker du eksempelet? Vi prøvde å finne ut hvorfor Danielle var så gretten, og hypotesen var at det skyldtes for lite søvn. Vi lagde et spredningsplott som viste sammenhengen mellom antall timer søvn og graden av grettenhet dagen etter (Figur 11.2 (b)), og fant en sterk negativ korrelasjon på r = -0{,}90.
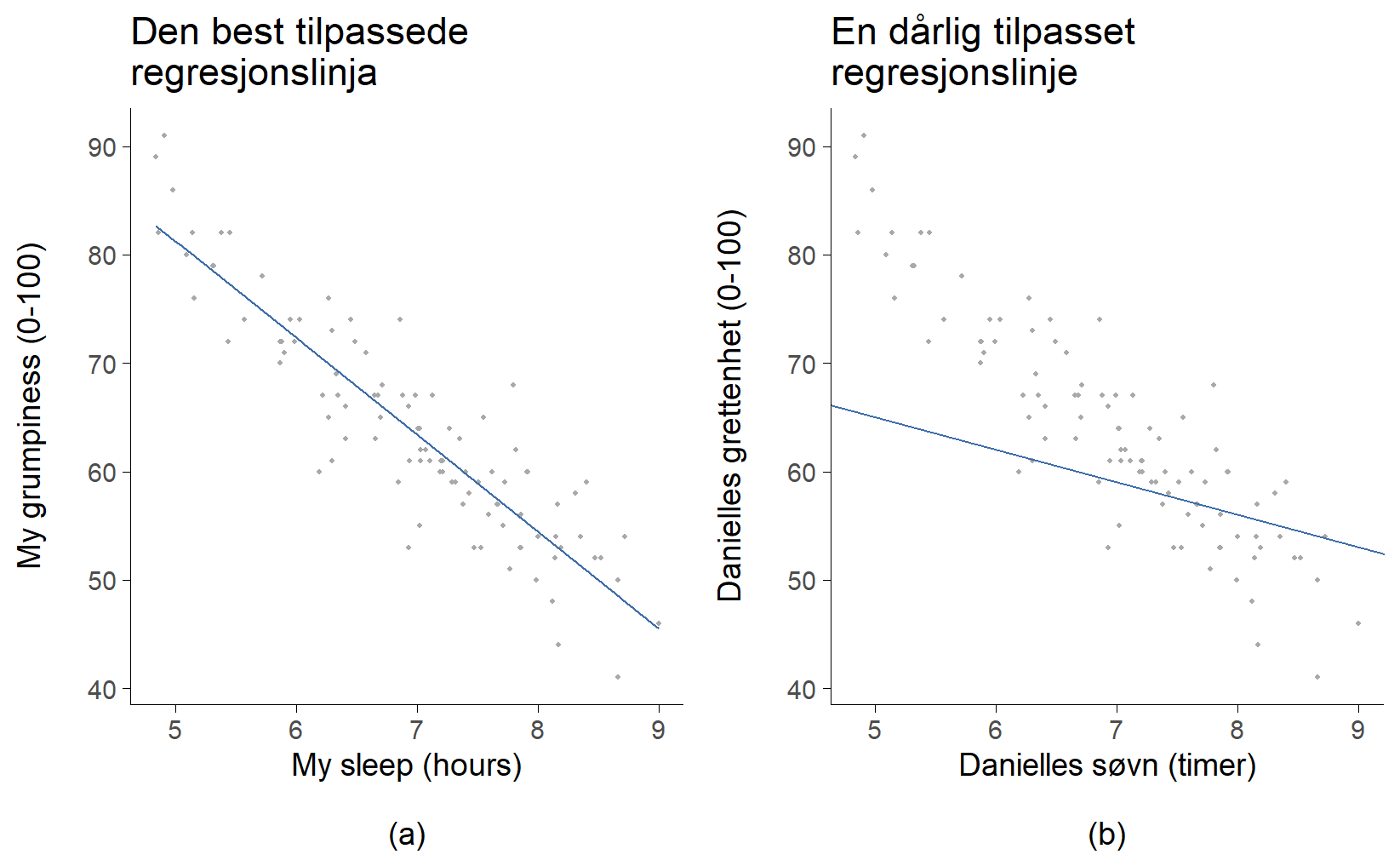
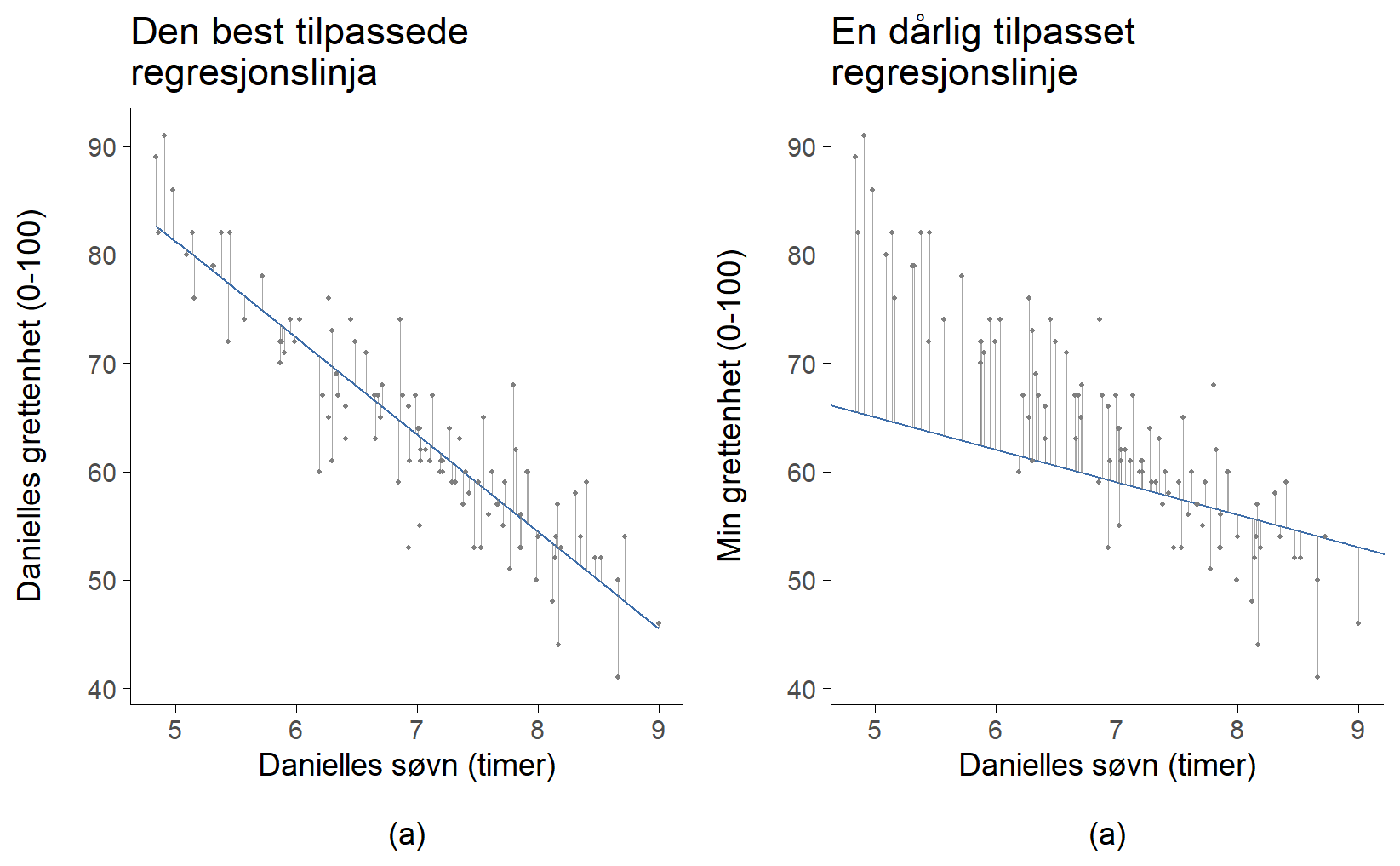
Når vi ser på et slikt plott, er det naturlig å forestille seg en rett linje som går gjennom midten av datapunktene, slik som i Figur 11.7(a). I statistikken kalles en slik linje for en regresjonslinje. Intuisjonen vår forteller oss at linjen bør følge trenden i dataene. Vi ville neppe tegnet en linje som den i Figur 11.7(b), som åpenbart ikke passer til punktene i det hele tatt.
Dette virker nok helt logisk. Linjen i Figur 11.7(b) passer rett og slett dårlig, så det gir liten mening å bruke den til å oppsummere dataene. Denne enkle observasjonen – at noen linjer passer bedre enn andre – er faktisk utrolig kraftfull når vi formaliserer den med matematikk.
For å komme dit, starter vi med en rask repetisjon fra matematikktimene på ungdomsskolen og videregående. Formelen for en rett linje skrives vanligvis slik:
y=ax + b
De to variablene er x og y, og vi har to koeffisienter, a og b. Koeffisienten b representerer konstantleddet, altså skjæringspunktet med y-aksen, og koeffisient a representerer stigningstallet til linjen. Konstantleddet tolkes som “verdien av y når x = 0”. Tilsvarende betyr et stigningstall på a at hvis du øker x-verdien med 1 enhet, øker y-verdien med a enheter. Et negativt stigningstall betyr at y-verdien vil synke.
Siden likningen y = ax + b kan beskrive alle rette linjer, bruker vi nøyaktig samme formel for en regresjonslinje. Det store spørsmålet er hvordan man kommer frem til den riktige regresjonslinja. Vi skal ikke lære å regne den ut, men vi skal lære prinsippet som ligger bak.
Prinsippet bygger på på avviket mellom linja og datapunktene, se Figur 11.8. Ser du at regresjonslinja ikke går gjennom de riktige y-verdiene, men at den bommer på alle punktene? Hvor mye linja bomma med har vi markert med mange grå linjer; hvis de grå linjene er lange, bomma regresjonslinja grovt, og hvis den er kort, bomma regresjonslinja lite. Lengden på de grå linjene markerer altså avviket mellom den y-verdien vi observerte og den y-verdien som regresjonslinja predikerer. Dette kalles residualet. Nå kan vi uttrykke prinsippet for hvordan man finner regresjonslinja: man finner den linja som totalt sett gir minst residualer. Og siden statistikere ser ut til å like å opphøye alt mulig i andre, av svært gode grunner, så blir definisjonen av regresjonslinja som følger:
Regresjonslinja y = ax + b har verdier for a og b slik at kvadratet av residualene blir minst mulig.
Dette betyr at linja i Figur 11.8 a) er regresjonslinja fordi residualene, de små grå linjene, er på sitt minste. Uansett hvilken annen linje du hadde valgt ville kvadratet av residualene vært større.
11.2.1 Lineær regresjon i jamovi
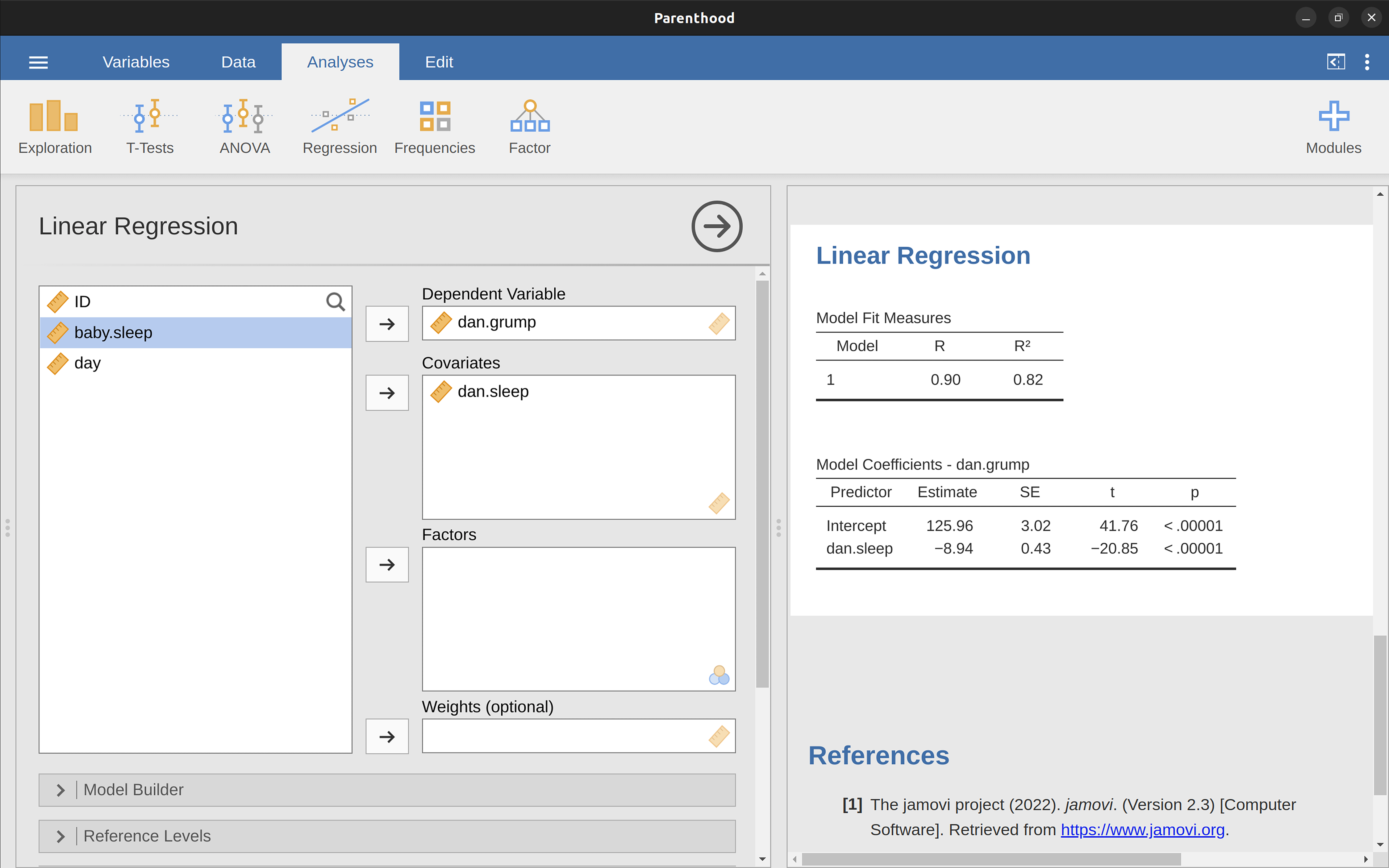
La oss utføre en enkel lineær regresjonsanalyse! For å gjøre dette, åpner du ‘Regression’ → ‘Linear Regression’-analysen i jamovi, ved å bruke datafilen parenthood.csv. Her spesifiserer du dani.grump som ‘Dependent Variable’ (avhengig variabel) og dani.sleep som ‘Covariates’. En “covariate” er bare et annet ord for uavhengig variabel.2
Dette gir resultatene vist i Figur 11.9. Vi ser vi har funnet et konstantledd (“intercept”) b = 125{,}96 og et stigningstall a = -8{,}94. Med andre ord, den best tilpassede regresjonslinjen vi plottet i Figur 11.8 kan uttrykkes med denne formelen:
y = 125{,}96 -8{,}94 x
Hvis man vil uttrykke det mer folkelig, kan man skrive:
\text{grettenhet} = 125{,}96 - 8{,}94 \cdot \text{timer søvn}
Det er noen tall til vi bør være oppmerksomme på, nemlig de som står øverst og som beskriver “Model Fit Measures”, altså mål på hvor godt denne modellen passer med dataene. Mer om disse i i neste delkapittel.
11.2.2 Å tolke resultatene fra regresjonen
Nå skal vi se på hvordan vi tolker disse koeffisientene – dette er en viktig del av analysen!
La oss begynne med a, altså stigningstallet. Som vi husker fra definisjonen, betyr en regresjonskoeffisient på a = -8{,}94 at for hver enhets økning i X (den uavhengige variabelen), forventer vi en reduksjon på 8{,}94 i Y (den avhengige variabelen). Overført til vårt eksempel betyr dette at for hver ekstra time søvn (dani.sleep) vi får, vil grettenheten (dani.grump) reduseres med 8{,}94 poeng. Det høres jo ut som en god ting for humøret!
Men hva med konstantleddet, b = 125{,}96? Siden b representerer den forventede verdien av y når x er lik 0, er tolkningen ganske enkel. I vårt tilfelle betyr dette at hvis vi får null timer søvn (X = 0), forventes grettenheten å være hele 125{,}96 poeng (y = 125{,}96). Dette er en ganske ekstrem verdi og understreker viktigheten av å få nok søvn -– best å unngå null timer, for humørets skyld! Mer seriøst understreker det at man i ikke bør spå verdier langt utenfor der man har data. Siden den minste verdien for x var 5, så da bør man ikke tolke konstantleddet, siden det tilsvarer x = 0.
Merk at jamovi også spytter ut en standardfeil (SE, “standard error”), en t-verdi og en p-verdi. Disse verdiene antar at datapunktene er hentet med enkelt tilfeldig utvalg fra en eller annen populasjon, og at man bruker dataene til å regne ut populasjonsparametre.
Våre data er ikke trukket enkelt tilfeldig, men er Danielles 100 første netter med spedbarnet sitt. For å avgjøre om testen jamovi spytter ut har noen mening bør vi vurdere om dette vil være “likt” et enkelt tilfeldig utvalg fra en eller annen populasjon. For meg høres det OK ut å si at disse 100 nettene er omtrent tilfeldig trukket fra “alle netter Danielle kommer til å ha med et spedbarn”. I så fall betyr \text{SE} = 0{,}43 at standardavviket til utvalgsfordelingen til a er 0{,}43, og at a er signifikant forskjellig fra null (t = -20{,}85, p < 0{,}00001). Dette er altså utsagn om populasjonen; hvis det i populasjonen “alle Danielles netter med spedbarn” er slik at a = 0 er det ekstremt lite sannsynlig å observere utvalget i våre data.
Du kan tilfreds legge merke til at denne testen også har t som testobservator, så forståelsen av t-verdier du bygde fra Kapitel 10 kan brukes flere steder.
Siden konstantleddet ikke burde tolkes så nøye i dette tilfellet unnlater jeg å tolke dets tester.
At vi har funnet en regresjonslinje betyr ikke at regresjonslinja passer godt til dataene. Det kan være observasjonene ligger tett rundt regresjonslinja, slik at den predikerer verdiene godt, eller det kan være observasjonene ligger langt unna regresjonslinja, slik at den predikerer dårlig. Vi trenger altså et mål på hvor tett rundt regresjonslinja punktene ligger. Heldigvis har vi det fra før av, det var det vi kalte (Pearsons) korrelasjon, r, se Seksjon 11.1.
Når jamovi viser tallet R under “Model Fit Measures”, så er dette ingenting annet enn korrelasjonen. Vel, nesten. R vil alltid være en positiv verdi, siden regresjonslinja passer like godt til dataene uansett om korrelasjonen er +0{,}9 eller -0{,}9. Det andre tallet, R^2 = 0{,}816, er bare kvadratet av R. Sukk, enda en kvadrering? Også denne kvadreringen er godt begrunnet, for R^2 har en veldig tilfredsstillende tolkning: den angir hvor stor andel av variansen i den avhengige variabelen som blir forklart av den uavhengige variabelen. I dette tilfellet: siden R^2 = 0{,}816, så blir 81,6% av variasjonen i Danielles grettenhet forklart av Danielles søvn.
11.3 Multippel lineær regresjon
Til nå har vi sett på den enkle lineære regresjonsmodellen, som typisk fokuserer på én enkelt prediktorvariabel – som i vårt eksempel var dani.sleep. Mange av de statistiske verktøyene vi har utforsket har antatt at du arbeider med én prediktor og én utfallsvariabel. Men i den virkelige verden er det sjelden så enkelt! Ofte har du flere faktorer som kan påvirke utfallet du studerer.
Heldigvis kan vi enkelt utvide den lineære regresjonen til å inkludere flere prediktorer. Dette er nettopp det multippel regresjon handler om! Konseptuelt er multippel regresjon overraskende enkelt. Alt vi gjør er å legge til flere ledd i regresjonsligningen vår. I stedet for y = ax + b der x er den eneste prediktoren, så kan man for eksempes inkludere tre prediktorer x_1, x_2 og x_3 slik: y = ax_1 + bx_2 + cx_3 + d
La oss si at vi ønsker å forstå grettenheten min (dani.grump) bedre. Tidligere så vi kun på min egen søvn (dani.sleep), men hva om sønnen min sin søvn (baby.sleep) også spiller en rolle? Hvis vi utfører en slik regresjon vil man ha ett stigningstall for dani.sleep og ett stigningstall for baby.sleep. Gir ikke det mening? Hvis Danielle sover dårlig, men babyen sover godt, vil ikke Danielle være like gretten som om begge sov dårlig. Derfor ønsker vi å bruke både dani.sleep og baby.sleep for å predikere Danielles grettenhet.
11.3.1 Multippel lineær regresjon i jamovi
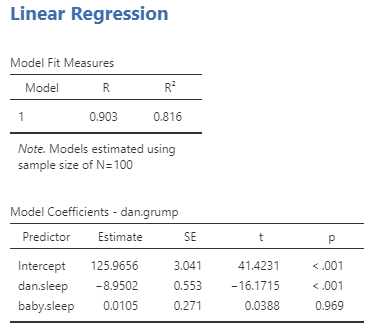
Multippel regresjon i jamovi er ikke annerledes enn enkel regresjon. Alt vi trenger å gjøre er å legge til flere variabler i ‘Covariates’-boksen i jamovi. For eksempel, hvis vi ønsker å bruke både dani.sleep og baby.sleep som prediktorer i vårt forsøk på å forklare hvorfor jeg er så gretten, så flytter vi baby.sleep over til ‘Covariates’-boksen sammen med dani.sleep. Som standard antar jamovi at modellen skal inkludere et konstantledd. Resultatene viser vi i Figur 11.10.
Stigningstallet knyttet til dani.sleep er ganske stor, -8{,}9502, noe som antyder at hver time jeg mister søvn gjør meg ordentlig gretten. Koeffisienten for baby.sleep er imidlertid veldig liten, noe som indikerer at det egentlig ikke spiller noen rolle for Danielle hvor mye søvn sønn hennes får. Hvis vi ser på den øverste tabellen, som viser hvor godt regresjonslinja passer til dataene, så ser vi at R^2 fremdeles er 0,816%, så regresjonsmodellen som inkluderer babyens søvn forklarte dessverre ikke noe mer av variasjonen i Danielles grettenhet.
Det var det! Multippel lineær regresjon er blant de virkelig store arbeidshestene i statistikken og passer i svært mange ulike sammenhenger.
11.4 Sammendrag
I dette kapittelet har vi sånn grovt sett dekket følgende:
- Vil du vite hvor sterk sammenhengen er mellom to variabler? Beregn korrelasjoner.
- Husk å tegne spredningsdiagrammer.
- Noen grunnleggende ideer om hva en lineær regresjonsmodell er.
- Hvordan man utfører regresjonen i jamovi og tolker resultatet.
- Hvordan man utvider modellen til en multippel lineær regresjon.
- Hvordan man tallfester hvor godt regresjonsmodellen passer ved hjelp av R^2.
Egentlig er selv den tabellen mer enn jeg ville giddet å lage. I praksis velger de fleste kun ett mål for sentraltendens og ett mål for variabilitet.↩︎
Hmm, jeg glemte av “kovariat” som et annet ord for uavhengig variabel i Tabell 3.1. La oss ikke skrive det inn for å ikke overlesse leseren! 🤷↩︎