| Land | Elev-ID | Skole-ID | Trinn | Kjønn | Forventet utdanning | Likestilling | Sosioøkonomisk status |
|---|---|---|---|---|---|---|---|
| Norge | 50650229 | 5065 | 9 | Jente | VGS | 49.42491 | -0.19319 |
| Norge | 51110306 | 5111 | 9 | Jente | Høyere utdanning | 65.70400 | -0.42087 |
| Spania | 50510309 | 5051 | 8 | Gutt | Kort utdanning | 55.03404 | 0.37849 |
| Norge | 50020211 | 5002 | 9 | Jente | Ungdomsskole | 37.63793 | 0.33421 |
| Norge | 50330313 | 5033 | 9 | Gutt | Kort utdanning | 37.63793 | -2.33108 |
5 Visualisere data
Above all else show the data.
– Edward Tufte 1
Når du skal analysere data er en av de viktigste oppgavene å visualisere dem. Å visualisere dataene er viktig av to hovedgrunner:
- For å forstå dataene dine: å tegne grafer hjelper deg med å forstå dataene dine bedre. Grafene kan brukes for å besvare forskningsspørsmål, de kan hjelpe deg med å oppdage interessante trekk ved dataene du ikke hadde forventet og de kan vise deg hvis noe er galt med dataene dine.
- For å kommunisere resultatene dine: Ved å vise data på en ryddig og visuelt tiltalende måte gjør du det lettere for leserne å forstå budskapet ditt, og kanskje å overbevise dem.
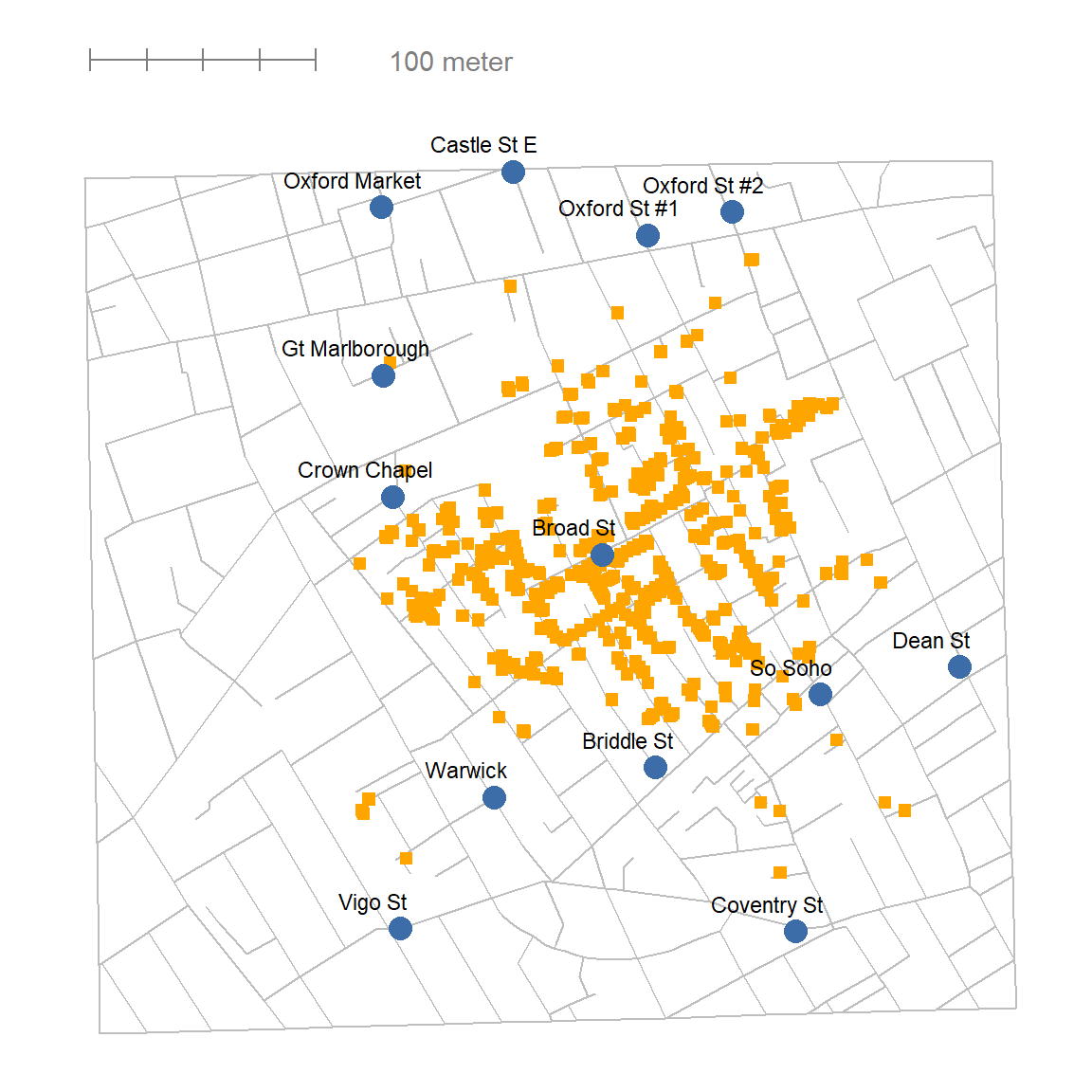
Det klassiske eksempelet for å vise hvor overbevisende og kraftfulle grafer kan være, er vist i Figur 5.1. Det er en stilisert versjon av en av de mest berømte grafene gjennom tidene – legen John Snow sitt kart over koleradødsfall fra 1854. Bakgrunnen er et kolerautbrudd som hadde tatt livet av over 500 personer. På den tiden forklarte man hvordan sykdommer smittet med miasme-teorien. Denne teorien hadde vært til stor hjelp og hjalp leger med gode tiltak mot mange sykdommer, for eksempel bruk av munnbind og begraving av lik langt unna folk. At sykdom kunne smitte via vann var uhørt, og John Snow vant ikke gjennom med argumentene sine om at kolera smittet fra vannpumpen på Broad Street. Derfor lagde han en figur. Figuren er elegant, det er rett og slett et gatekart som viser vannpumper (blå stor prikk) og addressen til personer som døde av kolera (gul liten prikk). Selv et kjapt blikk på grafen gjør det klart at vannpumpen i Broad Street er en mistenkt. Med figuren klarte han å overbevise myndighetene om å fjerne håndtaket på pumpen, noe som stoppet utbruddet. Slik er kraften i en god datavisualisering.
Vi viser deg de vanligste typene grafer og hvordan du lager dem i jamovi. I tillegg viser vi deg hvordan du kan lage undergruppeanalyser av grafene, noe som gjerne kan brukes for å besvare forskningsspørsmålene i en kvantitativ mastergrad. Grafene i seg selv er ikke så vanskelige å tolke, og jamovi gjør det enkelt å lage dem, så kapittelet er rett og slett ikke så vanskelig. Vi presenterer ikke hvordan man kan endre grafene, og muligens volder dette deg litt frustrasjon – man skulle jo så gjerne endret aksen slik og fargen slik – men jamovi har tilnærmet ingen muligheter for å endre på grafene. Programvaren prioriteter å gjøre det enkelt å lage standardgrafer i en tydelig og minimalistisk stil; hvis du vil gjøre noe ikke-standard, må du dessverre se deg om etter annen programvare.o
Og for ordens skyld, jeg kommer til å bruke graf, diagram, plott og visualisering om hverandre; jeg mener akkurat det samme med alle ordene.
5.1 Stolpediagram
For nominelle og ordinale data er stolpediagrammet det som er mest kjent. Vi fortsetter med ICCS-datasettet fra forrige kapittel, Kapitel 4. For å minne deg på hvilke variable datasettet inneholdt viser jeg de fem første radene.
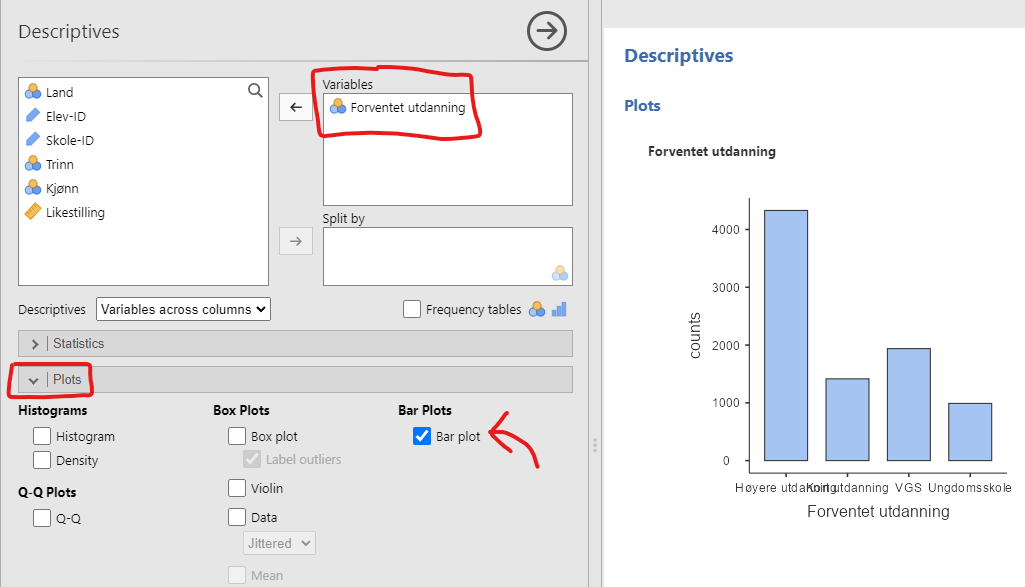
For å tegne et stolpediagram i jamovi trykker du “Analyses” → “Exploration” → “Descriptives” slik vi har gjort mange ganger før. Nå, derimot, må du trykke på “Plots” og krysse av for “Bar plot”, se Figur 5.2. I figuren har vi lagt til “Forventet utdanning” i variabelvinduet. Voilá, et flott stolpediagram. Siden “Forventet utdanning” er en ordinal variabel er stolpene tilogmed sortert i riktig rekkefølge.
Som du ser av figuren er den langt fra optimal – navnene på verdiene er så vide at de overlapper hverandre og blir uleselige! I jamovi er det ingen enkel måte å endre dette på. Det kanskje enkleste er å gå på “Variables” → “Edit” og skrive inn kortere navn på verdiene, for eksempel “Hø.Utd.” i stedet for “Høyere utdanning”. Der ser du med en gang hvor klønete det kan være å lage figurer i jamovi.
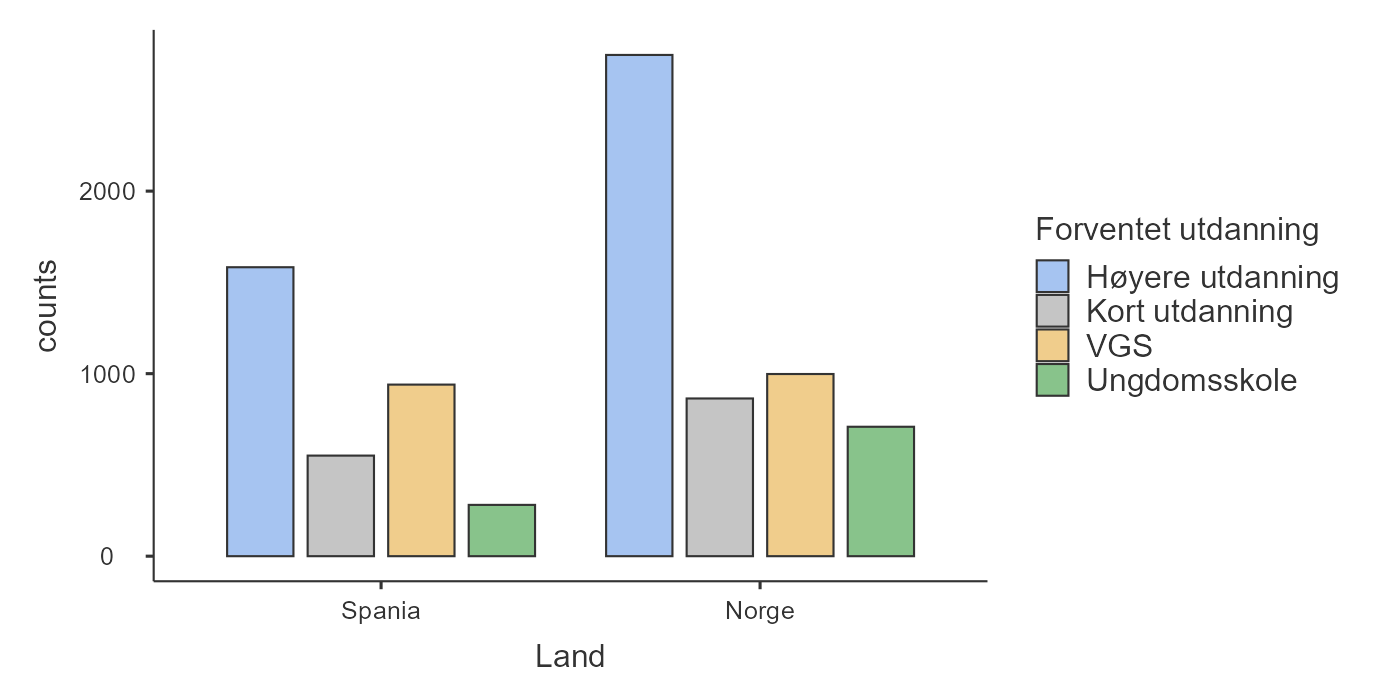
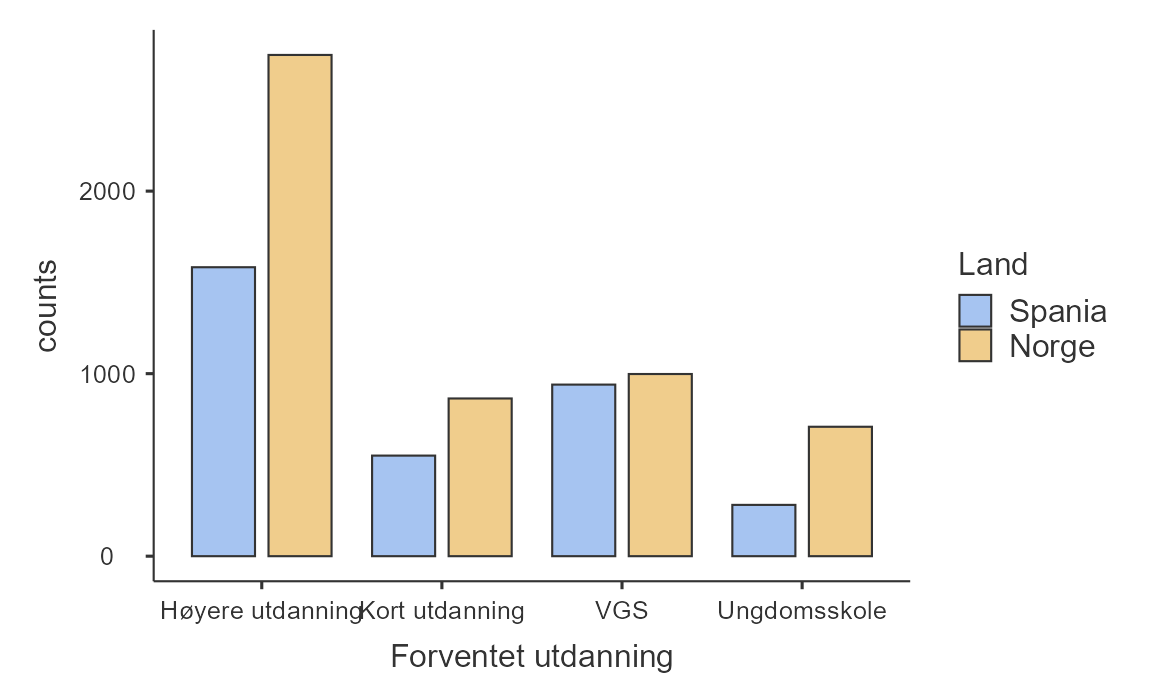
Hva med en undergruppe-analyse med stolpediagrammer? Da må vi legge til en variabel i “Split by”-vinduet. Vi legger til variabelen Land først, se Figur 5.3 (a). Wow, dette begynner allerede å se ganske bra ut! Hva med hvis vi bytter rekkefølge på variablene, altså har Land under “Variables” og Forventet utdanning under “Split by”? Se i Figur 5.3 (b). Hvis du lurer på hvilket du skal velge må du tenke over “hvilken kommuniserer best det poenget jeg prøver å få frem?” eller “hvilken besvarer forskningspørsmålet best?” Det er vanskelig å si generelt hva som er best.
Dette begynner allerede å se ganske bra ut!
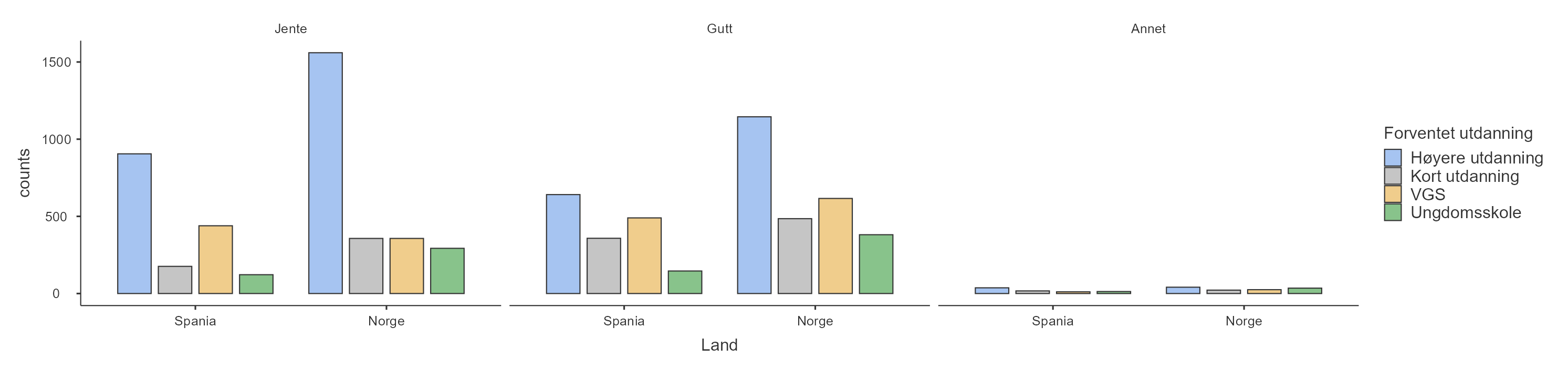
OK, nå fikk jeg blod på tann. Jeg vil gjøre undergruppeanalyse med enda en variabel! Jeg ønsker å se om det er kjønnsforskjeller i om elever ser for seg høyere utdanning i Spania og Norge, altså Forventet utdanning per Kjønn og Land. Vi legger ganske enkelt til enda en variabel i enten “Variables” eller “Split by”. På dette punktet bare sjonglerer jeg variable rundt mellom vinduene inntil jeg finner den figuren jeg liker best. I Figur 5.4 ser du resultatet av Land i “Variables” og Forventet utdanning og Kjønn i “Split by”.
Uff, det ble en koloss av en figur! Hvis du klarer å lese skriften vil du likevel se at den er ganske informativ. Vi skal forbedre den i neste delkapittel.
5.2 Stablede stolpediagram
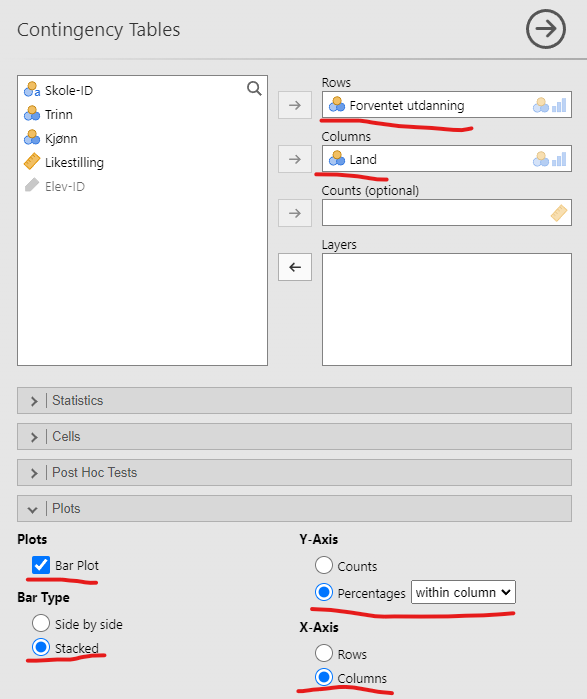
Stolpediagrammer kan stables oppå hverandre, noe som gjør dem mer kompakte og lettere å forstå, i noen sammenhenger. Vi trykker oss inn på en annen meny denne gangen, “Analyses” → “Frequencies” → “Independent samples (\chi^2 test of association)”. Her må du trykke deg inn på “Plots”, krysse av for “Bar plot”. I denne menyen er det mange flere innstillingsmuligheter enn før, se Figur 5.5:
- Jeg legger inn Forventet utdanning på “Rows” og Land på “Columns”. Dette er smak og behag for hvordan tabellen “Contingency Tables”, som også genereres, blir seende ut.
- Jeg velger “Bar Type: Stacked”, som altså betyr “Stolpetype: Stablet”.
- Jeg velger “Percentages” på “Y-axis”, fordi jeg ønsker å se andelen fra hvert land som ser for seg ulike utdanninger.
- Siden jeg ønsker å se andelen av hvert land, og jeg satte Land på “Columns”, må jeg velge “Percentages within column” for å regne prosenter for hvert land.
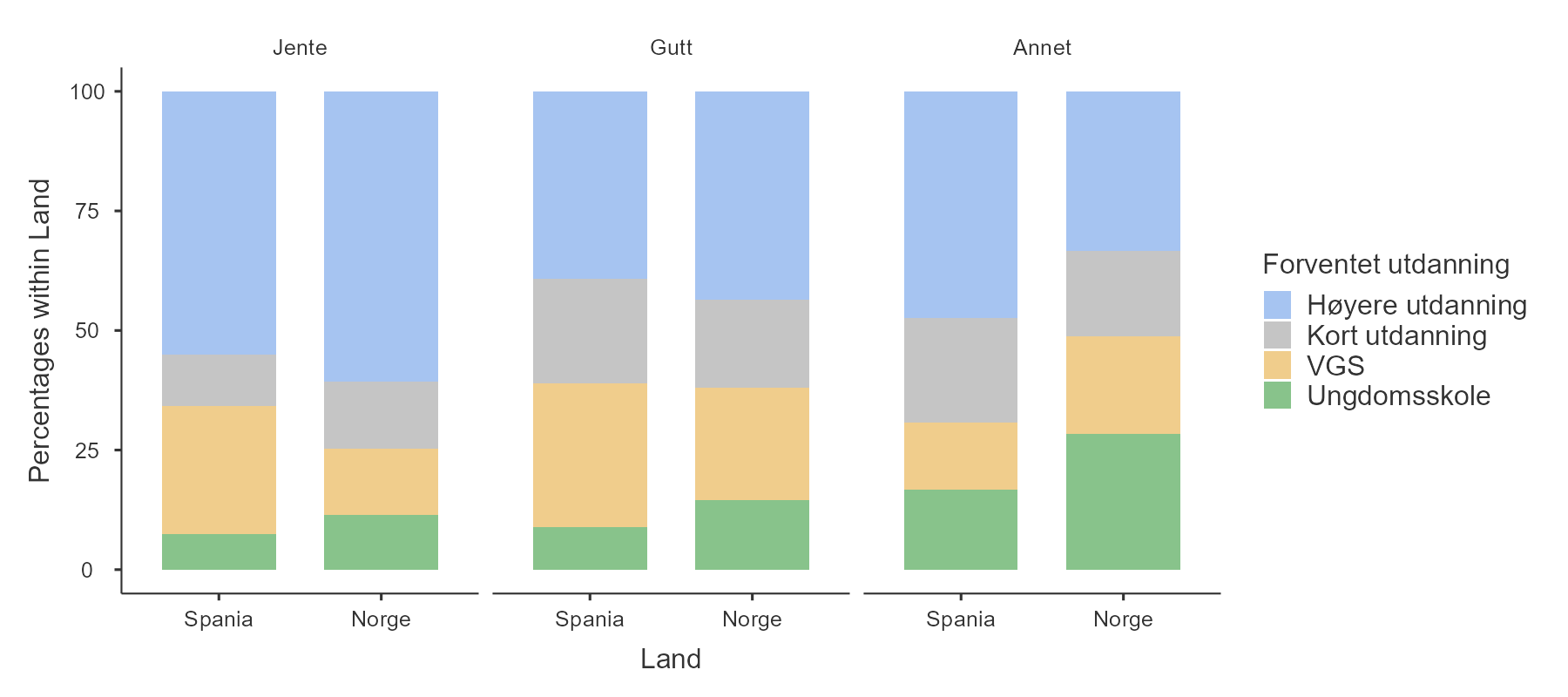
Resultatet ser du i Figur 5.6. Dette viser samme informasjon som Figur 5.3 (a), så du kan sammenligne og se hvilken du liker best. Forskjellen er at det stablede stolpediagrammet viser “andel innad i hvert land”. Her ser vi for eksempel at en noe større andel av de norske elevene planlegger høyere utdanning sammenlignet med de spanske elevene, men forskjellen er ganske liten. Hvis vi sammenligner med det vanlige stolpediagrammet, ser vi at dette viser absolutte tall. Der virker forskjellen mye større -– nesten dobbelt så mange norske som spanske elever ser for seg høyere utdanning! Grunnen til denne store forskjellen i stolpediagrammet er imidlertid at det er betydelig flere norske enn spanske elever i utvalget vårt (5317 mot 3355). Sannsynligvis er vi mer interessert i andelen elever som ser for seg høyere utdanning.
Nå kan vi igjen prøve å gjøre en undergruppeanalyse på tvers av to variable, Kjønn og Land. Kjønn ligger allerede under “Columns”, så vi legger inn Land under “Layers_. Resultatet blir som i Figur 5.7. Her skinner virkelig det stablede stolpediagrammet – se så kompakt og lesbart det ble i forhold til samme informasjon vist som et stolpediagram (Figur 5.7). Den største forskjellen mellom disse to diagrammene er at”Annet” var umulig å lese med det vanlige stolpediagrammet fordi stolpene ble så små, men med stablede stolper gikk det an å se at de de norske elevene som valgte annet i veldig stor grad ikke ser for seg mer skole etter ungdomsskolen. (Men husk at disse stolpene er basert på veldig få elever.)
Sånn, der var vi ferdig med stolpene! Og da var vi også ferdig med grafene for nominelle og ordinale variable, for de neste delkapitlene er for tall-variable.
5.3 Histogrammer
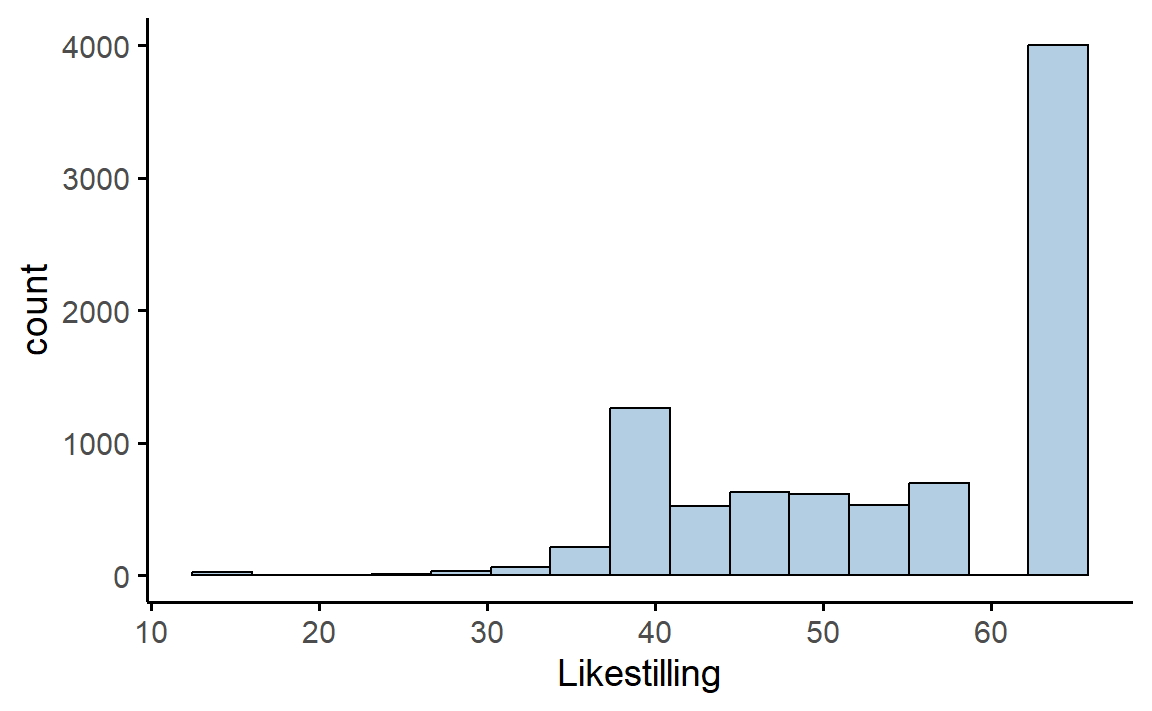
Histogrammer er blant de mest grunnleggende og nyttige måtene å visualisere data på. De fungerer best når du har tallvariable, altså data på intervall- eller forholdstallsnivå slik som variabelen Likestilling fra ICCS-dataene, og ønsker å få et overordnet inntrykk. De fleste kjenner nok til histogrammer, siden de brukes så ofte, men la meg likevel forklare hvordan de fungerer.
Prinsippet er enkelt: Du deler opp de mulige verdiene i intervaller og teller hvor mange observasjoner som faller innenfor hvert intervall. Denne tellingen kalles frekvensen eller tettheten til intervallet og vises som en vertikal stolpe. Jeg tror noe av grunnen til at de oppfattes som så enkle er at de minner om stolpediagrammer. For variabelen Likestilling finner vi for eksempel rundt 4000 elever som fikk max poengsum, noe som representeres av høyden på den høyre stolpen i histogrammet Figur 5.8, som vi også viste på starten av Figur 4.4.
For å lage dette histogrammet i jamovi trykker vi “Analyses” → “Exploration” → “Descriptives” og velger “Plots” og “Histogram”, se Figur 5.9.
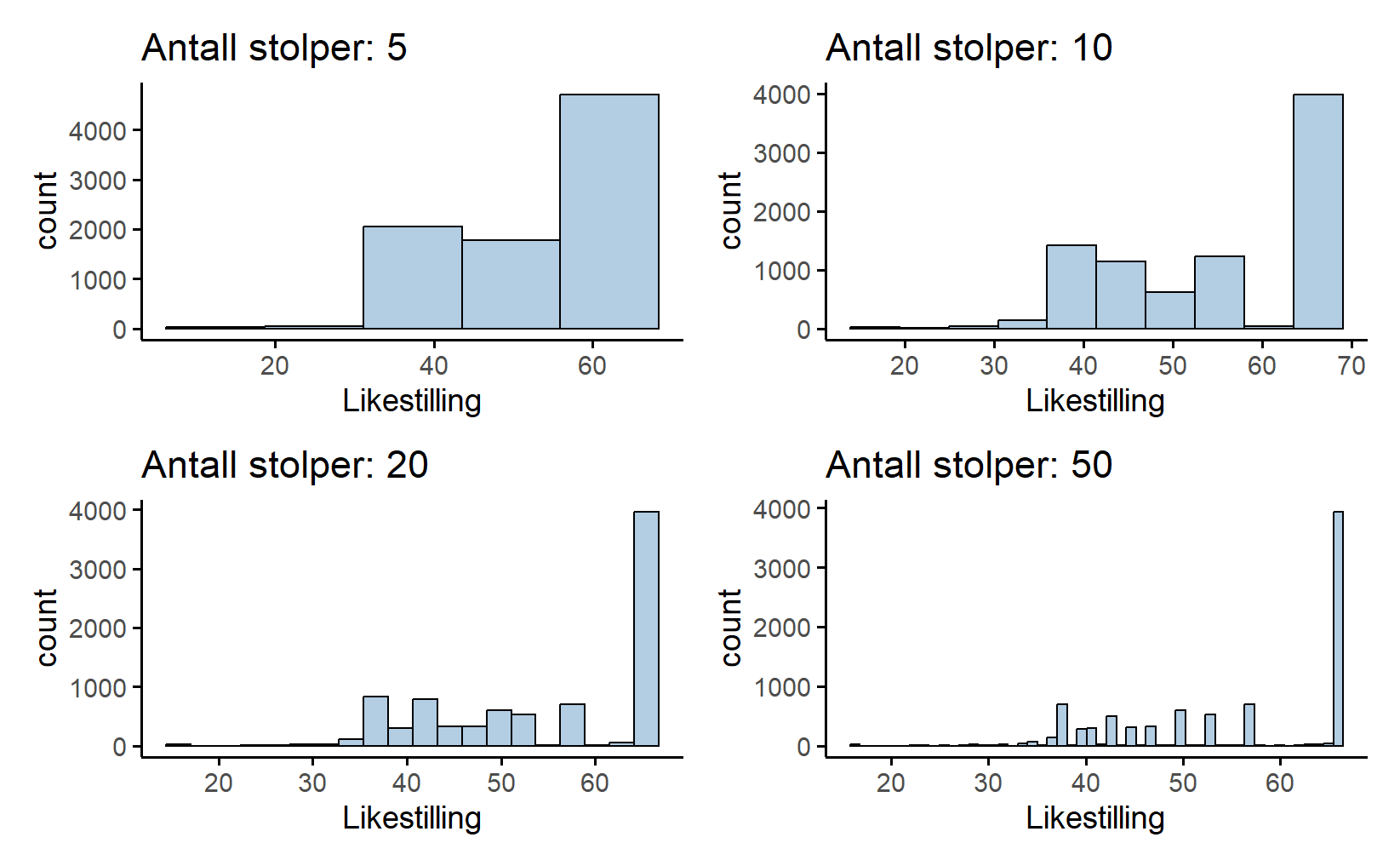
Problemet med histogrammer er at utseende deres er veldig avhengig av hvor mange stolper man lager. I Figur 5.10 ser vi den samme variabelen med litt forskjellig valg av antall stolper. De blir seende helt forskjellige ut.
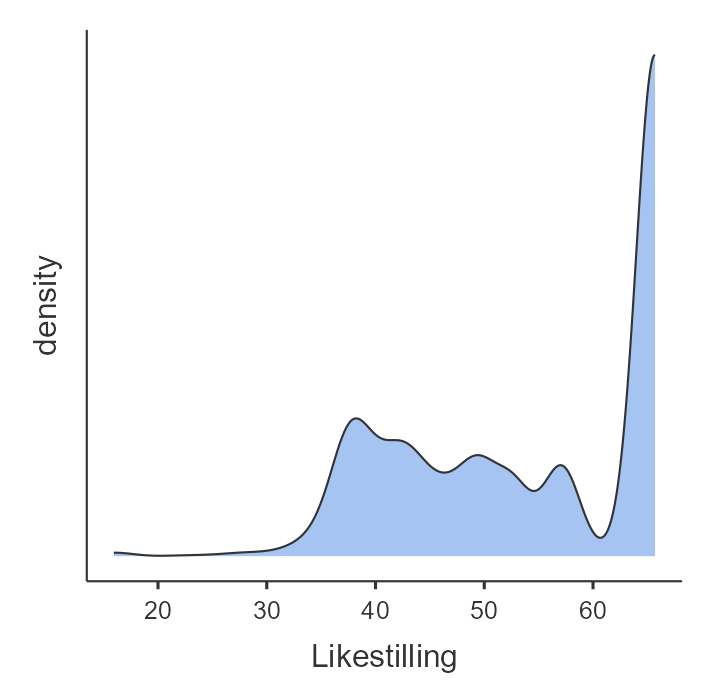
Et alternativ til histogrammer er tetthetskurver, noe som jamovi også tilbyr. Du kan gjøre dette ved å klikke på “Density”-avkrysningsboksen like ved “Histogram”-avkrysningsboksen. Resultatet vises i Figur 5.11.
En tetthetskurve visualiserer hvordan dataene fordeler seg kontinuerlig. Det benytter en matematisk teknikk for å lage en jevn kurve som viser hvor tett verdiene ligger. Toppene i et tetthetskurver viser altså hvor verdiene er tettest konsentrert, og dalene viser hvor det er få verdier. En fordel med tetthetskurver har over histogrammer er at den ikke påvirkes av antall søyler som brukes, slik som i et histogram. Grunnen til at jeg nevner tetthetskurver er fordi du ofte trenger å kunne tolke dem, for eksempel når du lærer om fiolinplott nedenfor.
5.4 Boksplott
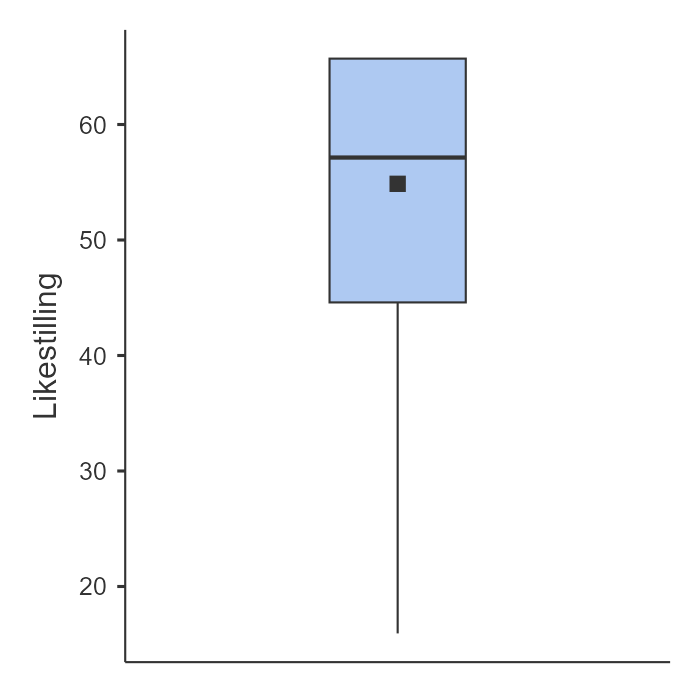
Et flott alternativ til histogrammer er boksplott. Ideen bak et boksplott er å gi deg en rask og tydelig visuell oversikt over medianen, kvartilbredden og variasjonsbredden i dataene dine. Siden denne informasjonen var enkel å regne ut også før datamaskiner ble vanlig, og fordi boksplott presenterer all denne informasjonen på en kompakt måte, er boksplott blitt populære – spesielt når du utforsker dataene for første gang og prøver å forstå hva de forteller deg. Vi tar en titt på variabelen Likestilling, se i Figur 5.12. For å lage et boksplott i jamovi trykker du på akkurat de samme knappene som for et histogram, du bare krysser av for “Box plot” i stedet for.
Den tykke linjen midt i boksen viser medianen. Av og til er det en firkantet stor prikk, og da viser den gjennomsnittet. Selve boksen dekker området fra 25. persentil til 75. persentil. De tynne linjene viser variasjonsbredden ved at de strekker seg ut til de mest ekstreme datapunktene i hver retning, i hvert fall nesten. Som vi skrev i Seksjon 4.4.1, så er variasjonsbredden veldig følsom for hvor ekstreme de mest ekstreme verdiene er. Derfor viser de fleste boksplott ikke variasjonsbredden, men kutter strekene ved en eller annen grense. Som standard er denne grensen satt til 1,5 ganger kvartilbredden (IQR). Hvis noen observasjoner faller utenfor dette området, vises de som prikker eller sirkler i stedet for. Disse kalles avviksverdier (outliers på engelsk). 2
I våre Likestilling-data er det ingen observasjoner som faller utenfor normalområdet, så det er ingen avviksverdier og derfor ingen prikker. En annen spesiell egenskap ved plottet er at det ikke er noen strek som går oppover. Grunnen til det er at det er ingen verdier som er høyere enn 75. persentil fordi det var så mange elever som fikk toppskår på Likestilling.
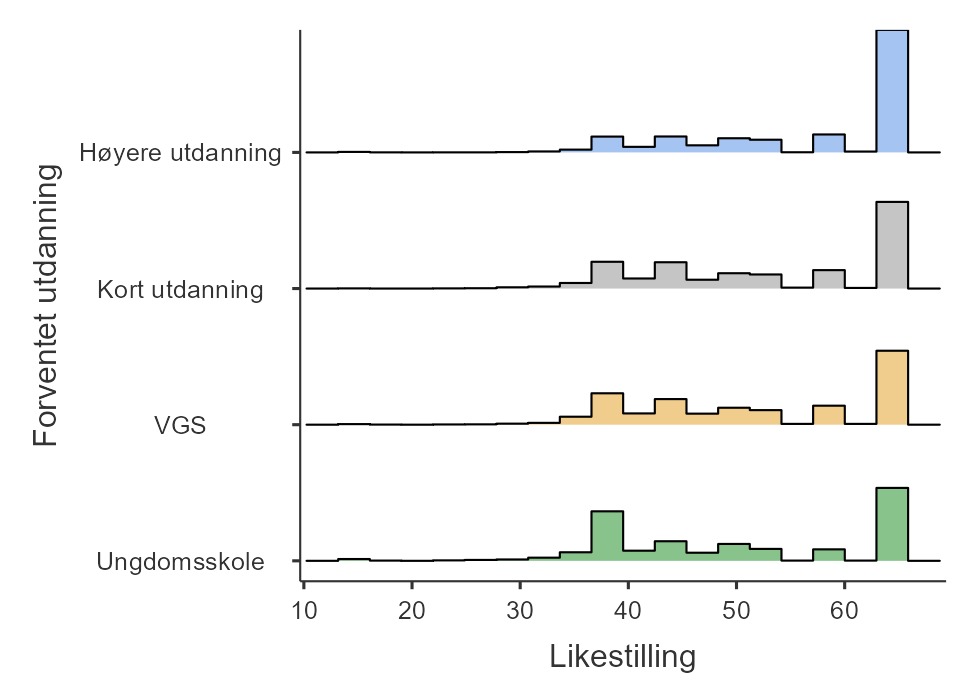
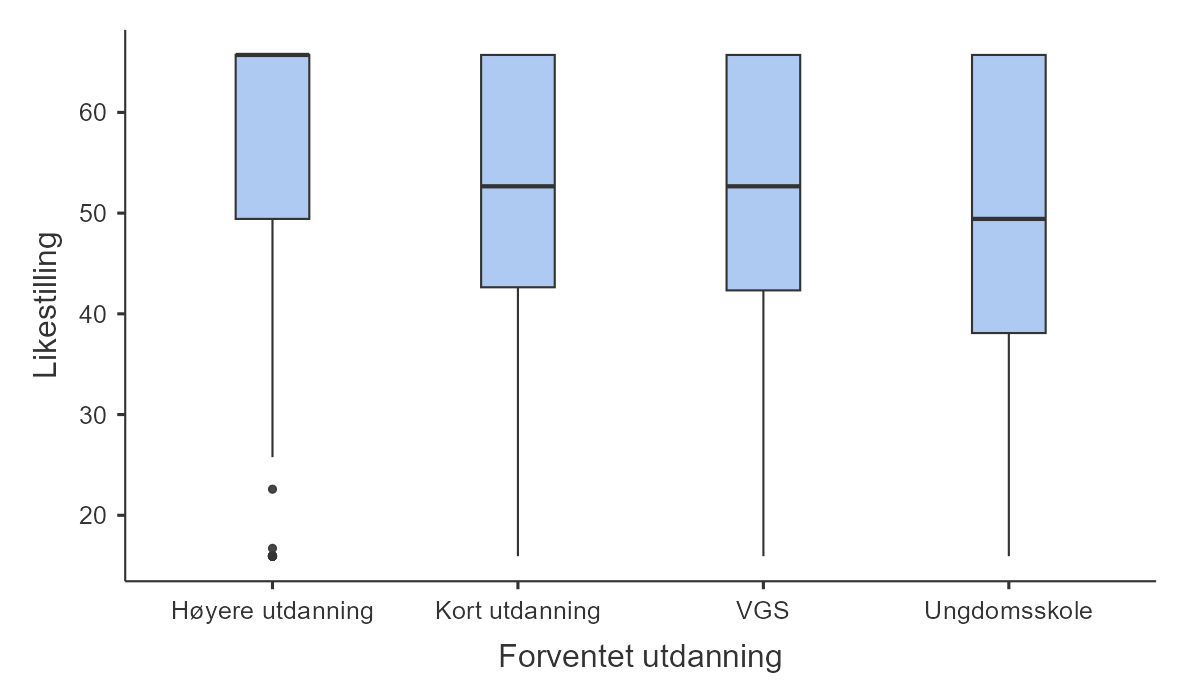
Du er kanskje ikke så imponert over boksplottet og synes histogrammet ga mer informasjon, og jeg er litt enig. Boksplottet viser riktignok medianen og kvartilbredden, men histogrammet viste mer nøyaktig hvordan verdiene fordelte. Boksplottet kommer til sin rett når man gjør en undergruppeanalyse, slik som i Figur 5.13. Det er rett og slett vanskelig å se forskjell på undergruppene med histogrammet, men med boksplottet er det lett å se at dess høyere utdanning eleven ser for seg, dess mer er eleven for likestilling mellom kjønnene. (Men merk at dette gjelder på gruppenivå og at det er mange unntak.) For å lage slike boksplott i jamovi er det bare å legge til en variabel i vinduet “Split by”.
I boksplottet i Figur 5.13 (b) ser du også hvordan avviksverdier ser ut med et boksplott, de er prikker som ligger utenfor halene.
5.4.1 Fiolinplott
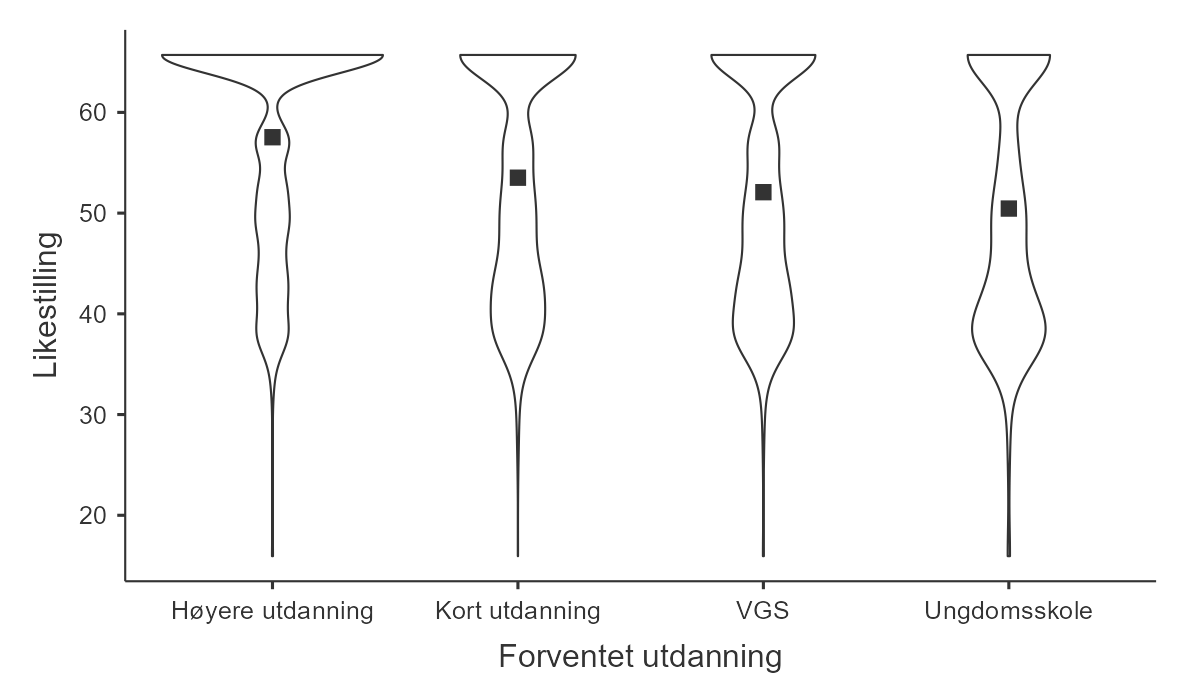
En moderne variant av det tradisjonelle boksplottet er fiolinplottet. Fiolinplott likner på tetthetskurver, men de er speilet slik at de ofte ser ut som en fiolinkropp. I jamovi kan du lage fiolinplott ved å krysse av for “Violin” i stedet for “Histogram”. Se Figur 5.14 for en undergruppeanalyse med fiolinplott. Her har vi også krysset av for at gjennomsnittet skal vises (på knappen står det “Mean”).
Fiolinplottet viser tydelig og kompakt hvordan verdiene fordeler seg. Hvis man i tillegg legger på informasjon som medianen eller gjennomsnittet kan man enkelt se forskjellene i sentraltendens mellom gruppene.
5.5 Spredningsplott
Så til den aller siste typen basisplott som vi skal gå gjennom, spredningsplott. Spredningsplott viser sammenhengen mellom to tallvariable. Histogrammer, boksplott og fiolinplott visualiserte én tallvariabel. Da jeg analyserte tallvariabelen opp mot andre variable, kalte jeg det en “undergruppeanalyse” og undergruppene var definert av en nominell eller ordinal variabel. Hva hvis du ønsker å gjøre en slags undergruppeanalyse definert av en tall-variabel? Da må du bruke et spredningsplott. La meg forklare.
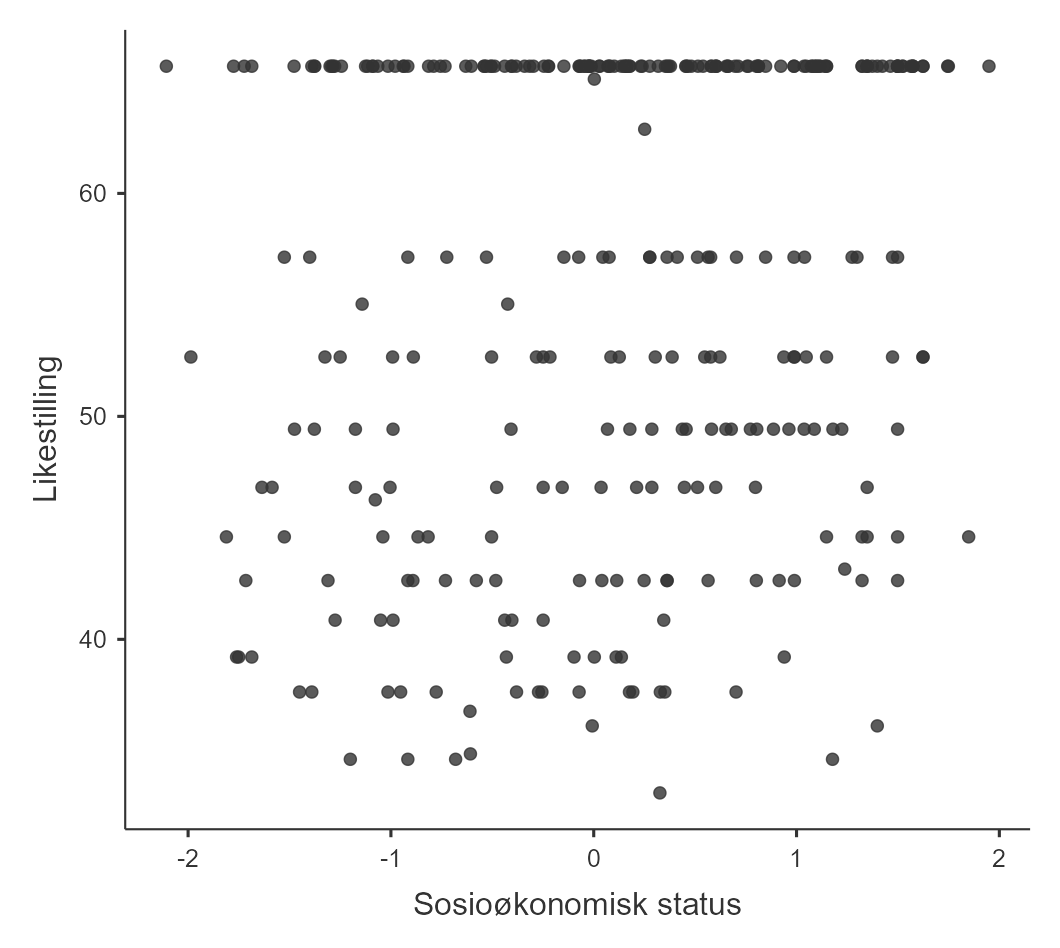
Vi har to tallvariable i vår versjon av ICCS-datasettet, Likestilling og Sosioøkonomisk status. Et naturlig spørsmål å stille er om elevene med ulik sosioøkonomisk status har forskjellig syn på likestilling mellom kjønnene. Hvis man prøver å gjøre en undergruppeanalyse der undergruppene er definert av Sosioøkonomisk status støter man på problemer, fordi det er 2029 ulike verdier av Sosioøkonomisk status. Man kan ikke vise så mange undergrupper! (De fem første verdiene i datasettet er -1.68595, 1.03747, 0.3034, -1.71153, -0.22118, skjønner du problemet, eller?)
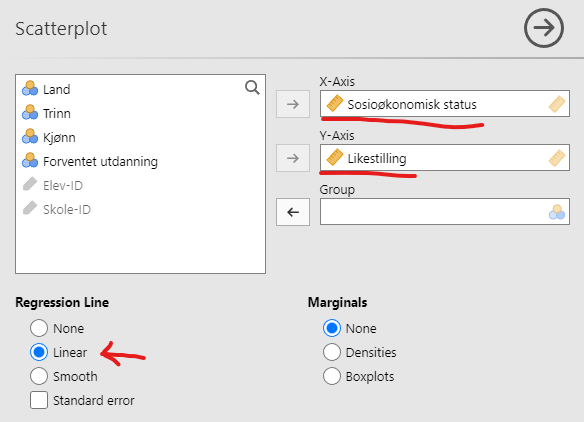
Løsningen er å legge hver sin variabel på hver sin akse og plotte hvert punkt. Hvis jeg vil legge Sosioøkonomisk status på x-aksen og Likestilling på y-aksen legger jeg inn dette i jamovi slik som i Figur 5.15 (a). Resultatet er i Figur 5.15 (b). Vi ser at uavhengig av sosioøkonomisk status virker den vanligste verdien på Likestilling å være den høyeste. Ut fra figuren er er det ikke klart om sosioøkonomisk status har noen sammenheng med syn på likestilling i det hele tatt.
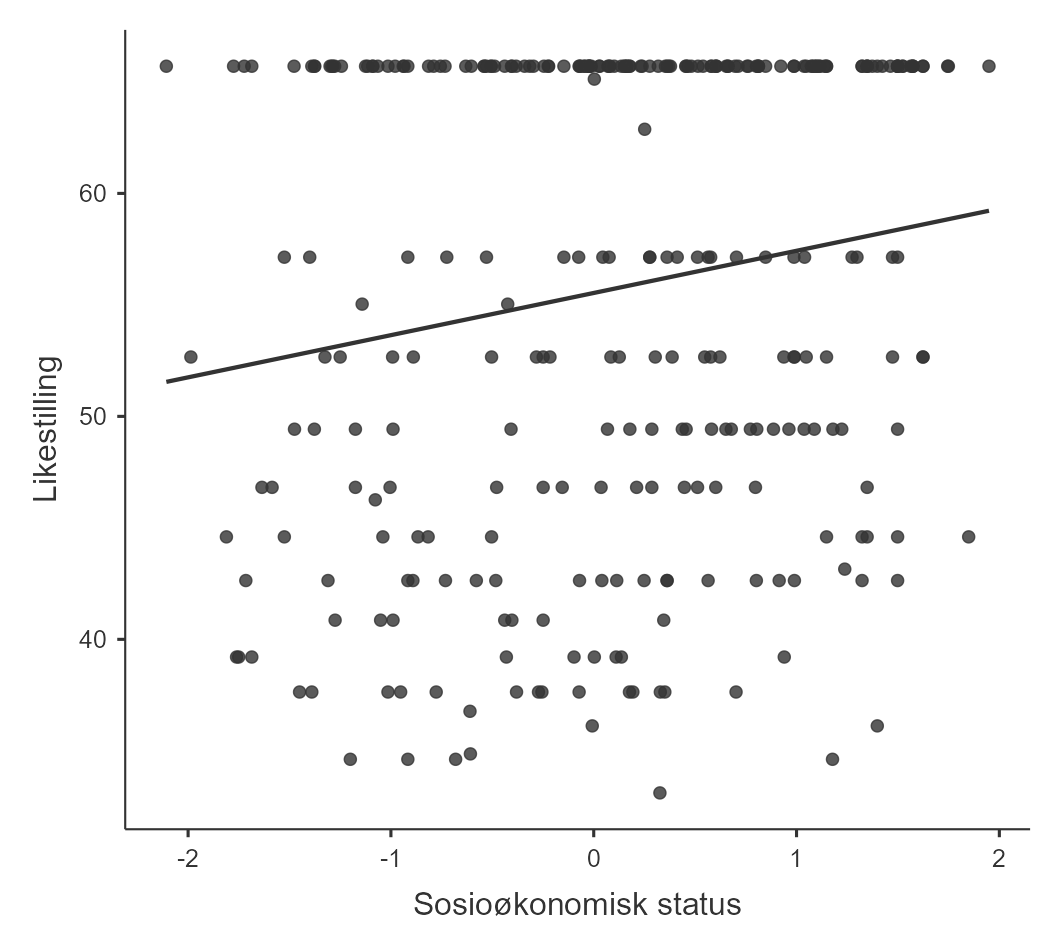
For å gjøre sammenhengen tydeligere er det vanlig å legge en linje over spredningsplottet, slik som i Figur 5.16. Den viser at det er en svak positiv tendens, altså at elever med høy sosioøkonomisk status svarer høyere på spørsmålene om likestilling. Du lærer mer om slike linjer, regresjonslinjer, i kapittelet om regresjon.
5.6 Profesjonelle grafer
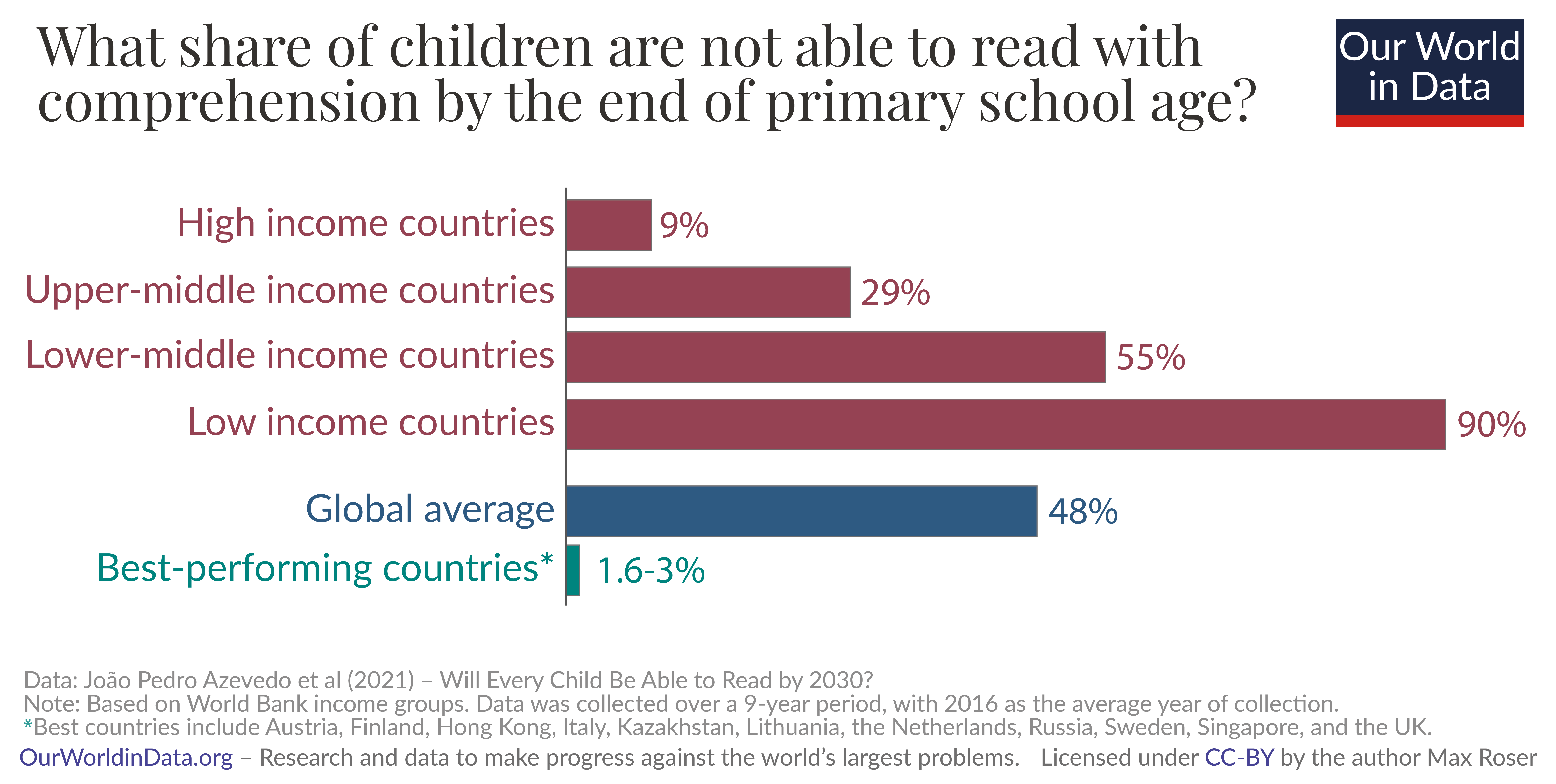
Jeg sa at jamovi tegnet standardgrafer som var tydelige og minimalistiske. Hva skiller dem fra mer forseggjorte grafer? Stort sett fargevalg og tekst-annoteringer som må skreddersys til hver graf. Se for eksempel på stolpediagrammet i Figur 5.17. Det er et vanlig stolpediagram, men
- det er lagt horisontalt slik at teksten skal bli lettere å lese,
- hver søyle er markert med prosenter,
- aksene er fjernet,
- farger er brukt for å vise grupper av søyler,
- Tittel og figurnoter forteller hele historien.
Alt i alt blir øyet ledet rundt i figuren slik at den samlet sett forteller en interessant historie om globale utdanningsforskjeller.
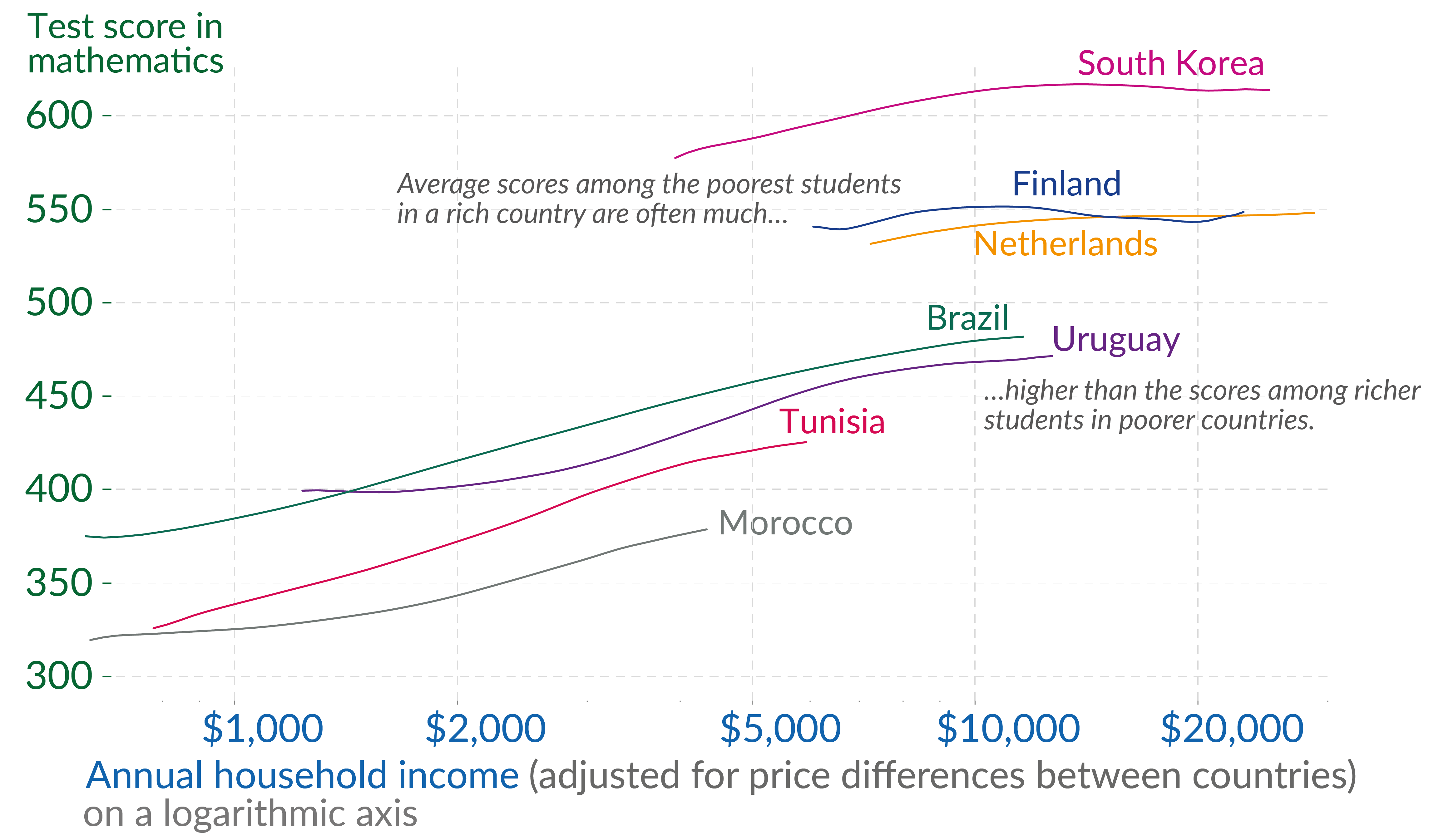
Det var et standard stolpediagram – andre diagrammer er spesiallagde. Se for eksempel på Figur 5.18, som på en fantastisk måte viser at ungene lærer mer i Sør-Korea, Finland og Nederland enn i Brasil og Uruguay, selv hvis man sammenlikner familier med samme kjøpekraft.
Andre visualiseringer er enda mer spesialiserte, som for eksempel for å vise hvordan amerikanere tilbringer dagene sine eller hele denne saken fra NRKs team med data-journalister som visualiserer naturnedbygging i Norge. Det er lov å la seg inspirere!
5.7 Lagre bildefiler med jamovi
Du lurer kanskje på hvordan du lagrer alle grafene vi har laget. Bare høyreklikk på grafen og eksporter det til en fil. Du kan velge mellom flere formater som “png”, “eps”, “svg” eller “pdf”. Alle disse formatene gir deg høy kvalitet på bildene, perfekt for å dele med kolleger, inkludere i oppgaver eller bruke i artikler og presentasjoner, men “.png” er trolig det som vil samarbeide best med Microsoft Word.
5.8 Sammendrag
Hjernen vår har en fantastisk kapasitet til å analysere data, men bare så lenge vi kan se på dataene i form av en graf. Hvis vi presenter informasjonen på riktig måte, gir vi leseren mye kunnskap på kort tid. Og den aller viktigste leseren av grafene du lager er deg selv – ved å lage mange grafer av dataene dine vil du skjønne dem bedre, oftere trekke velbegrunnede konklusjoner og sjeldnere trekke dårlig begrunnede konklusjoner. Derfor mener jeg dette er det viktigste kapittelet i boken hvis du skal gjøre kvantitativ forskning, i tillegg til Kapitel 2 og Kapitel 3.
I dette kapitlet har vi dekket:
- Vanlige plott: Vi har fokusert på standardgrafer som statistikere ofte bruker, som Stolpediagram, Stablede stolpediagram, Histogrammer, Boksplott (samt Fiolinplott) og Spredningsplott. Det er verdt å vite hvilke variabeltyper som passer til hver type plott, i tillegg til å kunne tolke dem.