10  Sammenlikne gjennomsnitt: ANOVA og paret t-test

Dette kapittelet introduserer to statistiske verktøy for å sammenlikne forskjeller i gjennomsnitt. Det første verktøyet, ANOVA, analyserer om gjennomsnittet er forskjellig i ulike grupper. Det andre verktøyet, paret t-test, kan brukes til å undersøke om gjennomsnittet har forandret seg mellom en før-test og etter-test.

10.1 Sammenlikne gjennomsnitt i ulike grupper: ANOVA

Vi starter med ANOVA, som står for “ANalysis Of VAriance”. Teknikken ble utviklet av Sir Ronald Fisher tidlig på 1900-tallet, og det er ham vi har å takke for den noe forvirrende terminologien. Begrepet ANOVA kan være litt misvisende på to måter. For det første handler ANOVA faktisk om å undersøke forskjeller i gjennomsnitt, selv om navnet refererer til varianser. For det andre finnes det flere forskjellige metoder som kalles ANOVA og som bare er løselig beslektet. Men i denne boka skal vi kun møte den enkleste formen for ANOVA, hvor vi har flere grupper av observasjoner og ønsker å finne ut om gjennomsnittet av en utfallsvariabel er forskjellig mellom gruppene. Denne varianten kalles for en “enveis ANOVA”.

Kapitlet er strukturert slik: Først introduserer jeg et fiktivt datasett som vi bruker som løpende eksempel. Deretter forklarer jeg hvordan en enveis ANOVA faktisk fungerer, før jeg viser hvordan du kan kjøre analysen i jamovi. Disse to seksjonene utgjør kjernen i kapitlet.

Advarsel

Fra og med dette kapittelet har jeg ikke rukket å gjøre eksemplene relevante for utdanningsvitenskap. Det er mye arbeid å finne relevante datasett fra utdanningsvitenskap og forklare analysene ved hjelp av dem, og det rakk jeg ikke før semesterstart for dette kapittelet. Derfor er eksempelet hentet fra originalboka Navarro & Foxcroft (2025), og omhandler psykofarmakologi, altså læren om medisiner for å behandle psykisk sykdom.

10.1.1 Et illustrerende datasett

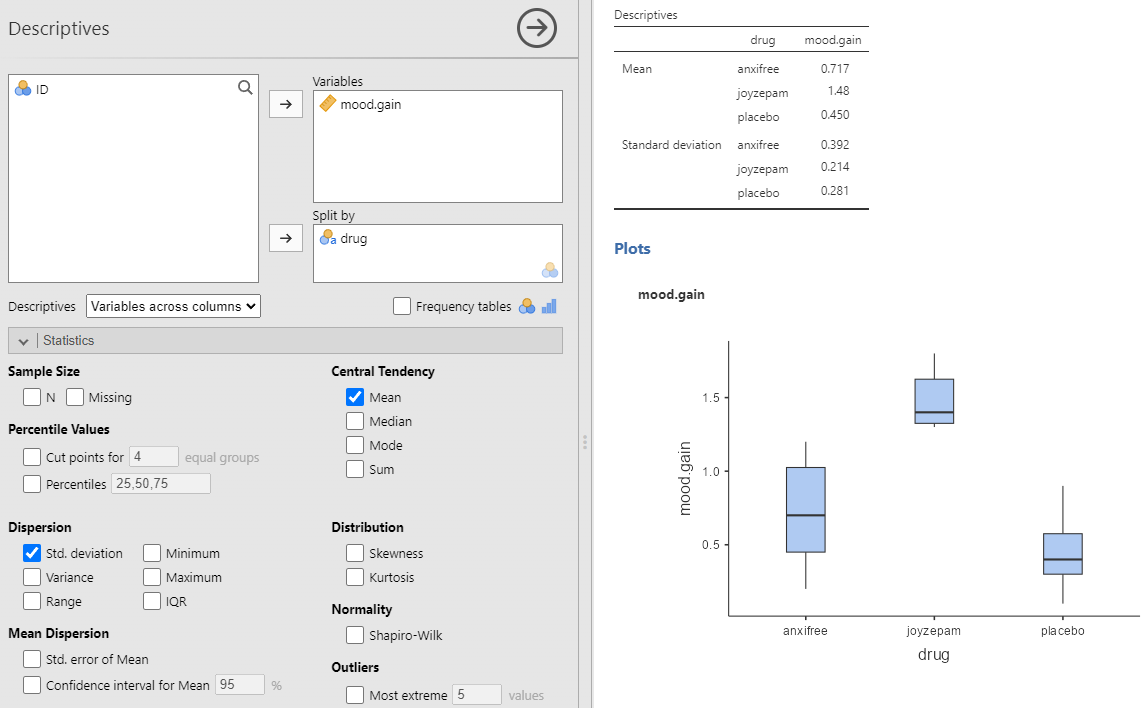
Anta at du har blitt involvert i en klinisk studie hvor du tester et nytt antidepressivt legemiddel kalt Joyzepam. For å teste medisinens effektivitet, inkluderer studien tre separate medikamenter. Ett er et placebo, altså luretabletter som ikke inneholder medisin, og det andre er et eksisterende antidepressivt/angstdempende medikament kalt Anxifree. En samling av 18 deltakere med moderat til alvorlig depresjon er rekruttert til den innledende studien. Siden medikamentene noen ganger gis sammen med psykologisk terapi, inkluderer studien 9 personer som gjennomgår kognitiv atferdsterapi (cognitive behavioral therapy, CBT) og 9 som ikke gjør det. Deltakerne blir tilfeldig tildelt en behandling, slik at det er 3 CBT-personer og 3 personer uten terapi tildelt hver av de 3 medikamentene. Utfallsvariabelen er at en psykolog vurderer humøret til hver person før og etter en 3-måneders periode med hvert medikament, og den samlede forbedringen i hver persons humør vurderes på en skala fra -5 til +5. Med dette som studiedesign, endte dataene opp som i datafilen clinicaltrial.csv, se Vi kan se at dette datasettet inneholder de tre variablene drug, therapy og mood.gain.

Tabell 10.1. Datafilen for den kliniske studien.

ID	drug	mood.gain
1	placebo	0.5
2	placebo	0.3
3	placebo	0.1
4	anxifree	0.6
5	anxifree	0.4
6	anxifree	0.2
7	joyzepam	1.4
8	joyzepam	1.7
9	joyzepam	1.3
10	placebo	0.6
11	placebo	0.9
12	placebo	0.3
13	anxifree	1.1
14	anxifree	0.8
15	anxifree	1.2
16	joyzepam	1.8
17	joyzepam	1.3
18	joyzepam	1.4

Vi er først og fremst interessert i effekten av drug på mood.gain. Slik vi lærte i Kapitel 4 er det alltid lurt å starte med å regne ut litt deskriptiv statistikk og tegne noen grafer for å skjønne dataene bedre, se Figur 10.1. Som plottet tydelig viser, er det en større forbedring i humør for deltakere i Joyzepam-gruppen enn for både Anxifree-gruppen og placebo-gruppen. Anxifree-gruppen viser en større humørforbedring enn kontrollgruppen, men forskjellen er ikke så stor. Spørsmålet vi ønsker å besvare er om disse forskjellene i gjennomsnitt er så store at det er usannsynlig å få så store forskjeller hvis gjennomsnittlig effekt egentlig er lik.

Figur 10.1. Deskriptiv statistikk og boksplott for humørforbedring for hvert medikament

10.1.2 Nullhypotesen og alternativhypotesen

Det eksperimentelle designet vi beskrev tidligere viser tydelig at vi ønsker å sammenligne den gjennomsnittlige humørforandringen mellom tre forskjellige medisiner. Det er akkurat slike forskningsspørsmål man undersøker med enveis ANOVA. Hvis vi analyserer dette oppsettet har vi to variable; vi har én variabel på forholdstallsnivå, mood.gain, og én kategorisk variabel, drug. En enveis ANOVA analyserer altså sammenhengen mellom en variabel på forholdstallsnivå og en kategorisk variabel. I vårt tilfelle har den kategoriske variabelen 3 kategorier, men den kan ha så få som 2 kategorier og det er ingen øvre grense for hvor mange kategorier den kan ha.

Den noe pessimistiske nullhypotesen vi ønsker å teste er at gjennomsnittlig mood.gain er lik for alle de tre medisinene – altså at ingen av medisinene er mer effektive enn placebo:

H_0: Gjennomsnittet av mood.gain er likt for de tre medisinene

Den alternative hypotesen er at minst én av de tre behandlingene skiller seg fra de andre.

H_1: Minst én av gjennomsnittene er ulik de andre

Denne nullhypotesen er betydelig mer kompleks å teste enn de vi har sett tidligere. Gitt kapitteltittelen vil du kanskje gjette at løsningen er å “gjøre en ANOVA”, men det er ikke umiddelbart opplagt hvorfor “analyse av varianser” kan hjelpe oss å lære noe om gjennomsnitt. Men vi vet at det vi må gjøre er å konstruere en passende testobservator.

10.1.3 Testobservatoren F og dens utvagsfordeling

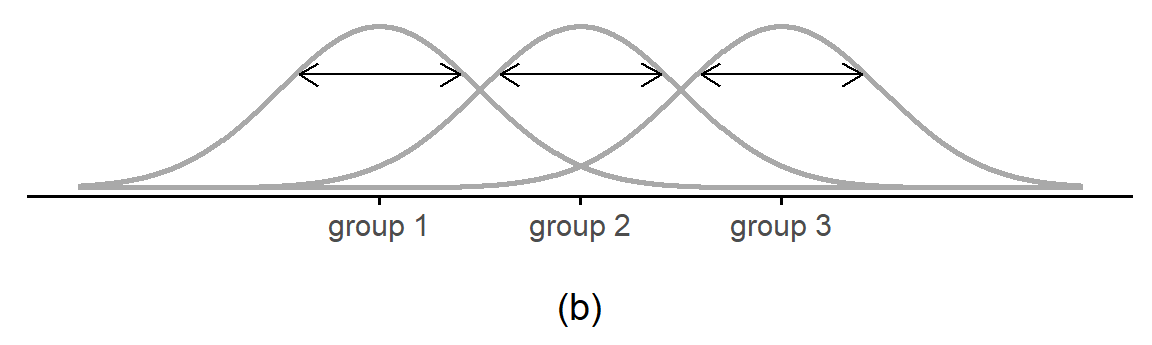
For å forstå hvordan dette fungerer, la oss begynne med å snakke om varianser. I ANOVA skiller man mellom to typer varianser, variansen mellom gruppene og innad i gruppene (Figur 10.2). Variansen mellom gruppene vises i Figur 10.2 (a) som piler mellom gruppenes gjennomsnitt. Dess lengre piler, dess mer variasjon mellom gruppene. Variansen innad i gruppene vises i Figur 10.2 (b) som bredden på hver gruppes fordeling; dess bredere fordeling (lengre piler), dess mer varians. I denne figuren er pilene for variansen mellom gruppene og innad i gruppene ca. like store. Legg også merke til at de tre gruppenes fordeling overlapper ganske masse. Det virker ikke helt usannsynlig at gruppenes gjennomsnitt er like i populasjonen, og at forskjellen mellom gruppene skyldes at man er litt uheldig med det utvalget.

(a) Variasjonen mellom gruppene er et mål på avstanden mellom gjennomsnittene

(b) Variasjonen innad i gruppene er et mål på hvor bred fordelingen er i hver gruppe

Figur 10.2. Grafisk illustrasjon av variansen mellom gruppene og innad i gruppene. Til venstre viser pilene forskjellen mellom gruppenes gjennomsnitt. Til høyre viser pilene variabiliteten innen hver gruppe

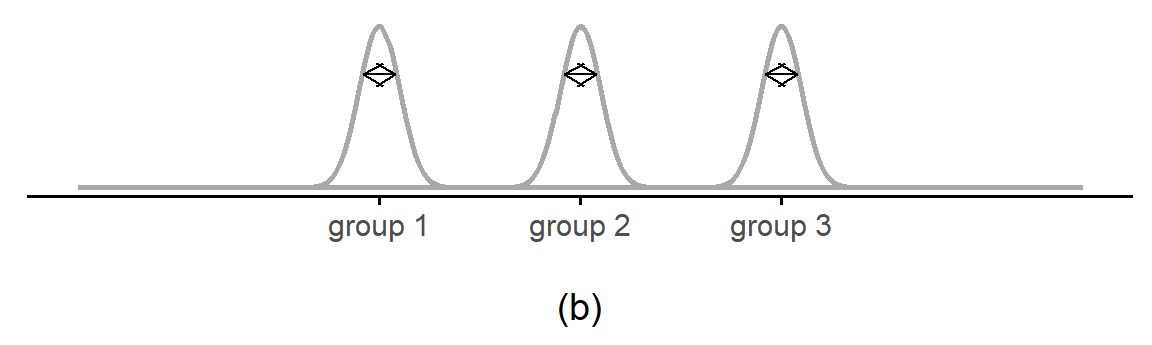
Situasjonen er motsatt i Figur 10.3. I denne figuren har de tre gruppene samme gjennomsnitt, men variasjonen innad i hver gruppe er mye mindre. Variasjonen mellom gruppene er like stor som før, Figur 10.3 (a), men variasjonen innad i gruppene er mye mindre, Figur 10.3 (b). Derfor virker det helt usannsynlig at de tre gruppene har samme gjennomsnitt i populasjonen.

(a) Variasjonen mellom gruppene er uendret, men fremstår større siden variasjon innad i gruppene er mindre

(b) Variasjonen innad i gruppene er mye mindre

Figur 10.3. Når variasjonen innad i gruppene er liten fremstår variasjonen mellom gruppene som veldig mye større. I dette eksempelet virker det helt usannsynlig at det ikke er noen forskjell mellom gruppene i populasjonen.

Moralen er at når man analyserer forskjeller i gruppers gjennomsnitt, så må man ikke bare ta hensyn til hvor forskjellig gruppenes gjennomsnitt er, man må også ta hensyn til hvor mye spredning det er innad i gruppene. Denne informasjonen fanges opp i F-observatoren, som er testobservatoren til en ANOVA. Hvis man glatter over alle detaljene kan man si at den regnes ut slik:

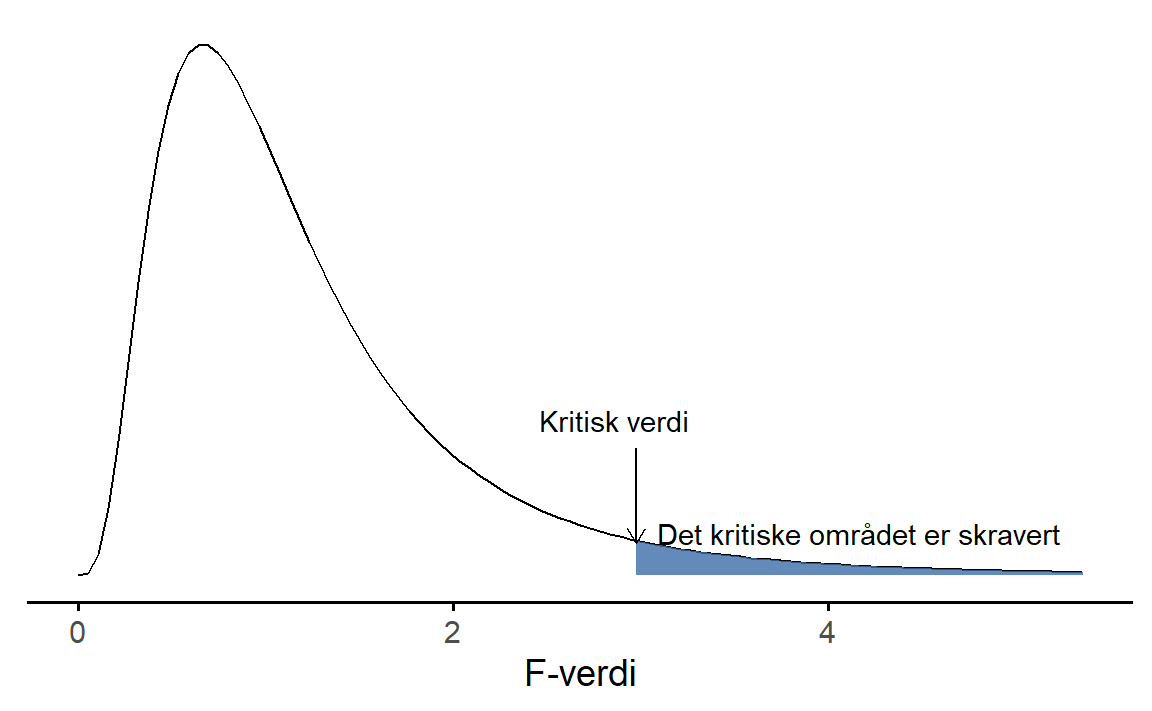
F = \frac{\text{variasjonen mellom gruppene}}{\text{summen av variasjonene innad i gruppene}}. Vi hopper over mange detaljer slik som spesifikke utregninger og at F-fordelinger har to frihetsgrader, men vi viser en F-fordeling der frihetsgrad nummer 1 er 10 og frihetsgrad nummer 2 10, se Figur 10.4.

Figur 10.4. F-fordeling og forkastningsområdet for en F-test.

10.1.4 Å gjennomføre ANOVA i jamovi

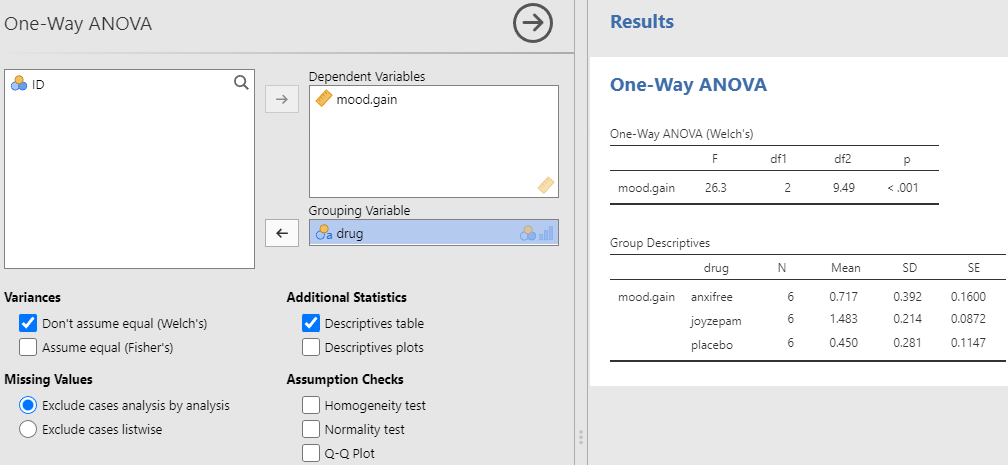
For å gjøre livet enklere kan jamovi utføre ANOVA for deg – hurra! Trykk på ‘ANOVA’ → ‘One-way ANOVA’, og flytt mood.gain-variabelen til ‘Dependent Variable’-boksen og deretter drug-variabelen over til ‘Fixed Factors’-boksen. Dette gir deg resultatene som vist i Figur 10.5. Resultatene viser F-verdien, samt begge frihetsgradene. Disse trenger ikke vi fokusere så mye på. Den oppgir også p-verdien, som i dette tilfellet er p < 0{,}001.

Figur 10.5. Resultater fra ANOVA i jamovi om humørforbedring etter å ha fått ulike medikamenter

Vi kan rapportere denne analysen slik:

Vi gjennomførte en ANOVA-analyse for effekten av medikament på humørforbedring og fant en signifikant effekt (F = 26.3, df1 = 2, df2 = 9{,}49, p < 0{,}001).

Merk at disse resultatene ikke sier noe om hvilken av medikamentene som hadde størst og minst gjennomsnitt, den sier bare at vi forkaster hypotesen om at gjennomsnittet på utfallsvariabelen var lik i de tre gruppene. For å finne ut av hvilket medikament som var mest effektivt kan man titte på den deskriptive statistikken som jamovi tilbyr ved knappen “Descriptive table”. Vi ser at de som fikk anxifree hadde en humørbedring på 0,717; de som gikk på joyzepam 1,483; og de på placebo 0,450. Joyzepam var altså det mest effektive legemiddelet. Merk at jamovi oppgir både standardavviket (SD) og standardfeilen (SE). ¹

Med disse tallene kan vi rapportere videre:

Effekten av joyzepam ga en humørforbedring på 1,48 95% CI [1,31; 1,65], som var større enn både anxifree (0,72 95% CI [0,41; 1,03]) og placebo (0,45 95% CI [0.23; 0.67]).

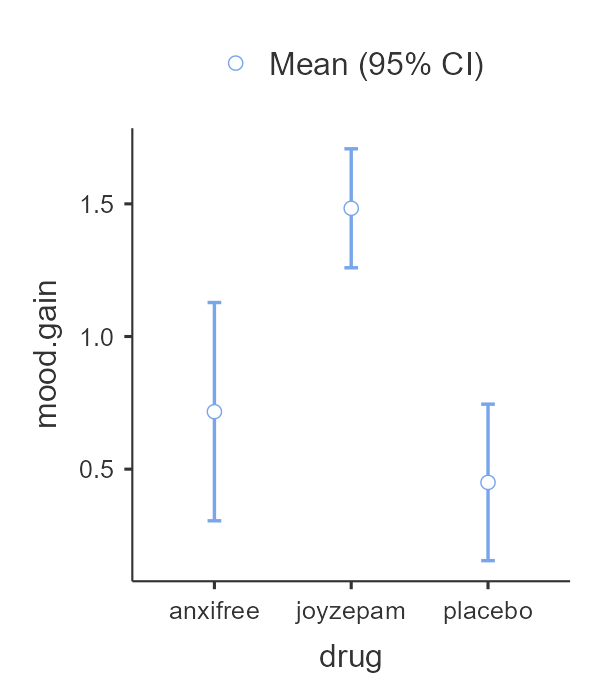
Det er lettere å sette seg inn i resultatene med en visualisering, så jeg viser også hva jamovi tilbyr under “Descriptives plots” i menyene til enveis ANOVA, se Figur 10.6. Her vises gjennomsnittene med en prikk og 95% konfidensintervall er vist med streker. Merk at konfidensintervallet er ca. 2 standardfeil, slik vi lærte i Seksjon 7.5.

Figur 10.6. Et plot med gjennomsnitt og konfidensintervall for humørforbedring etter å ha fått ulike medikamenter

Hvis ANOVA-analysen er den sentrale analysen i artikkelen din bør du trolig legge ved en liknende visualisering.

10.2 Sammenlikne gjennomsnittlig forbedring: paret t-test

Paret t-test sammenlikner gjennomsnitt på tvers av to grupper, men der hver observasjon i den første gruppen svarer til en observasjon i den andre gruppen. Dette er en litt tungvindt måte å snakke på, så vi skal begrense oss til kun én slik situasjon, endring mellom en før-test og ettertest. Her er observasjonene naturlig delt i to grupper, før og etter, og hver deltager har en måling for både før-testen og for etter-testen.

10.2.1 Dataene

Datasettet vi skal bruke denne gangen kommer fra Dr. Chicos sin undervisning. I klassen hennes tar studentene to store tester – en tidlig i semesteret og en senere i semesteret. Dr. Chico sine timer er utfordrende og studentene bør jobbe mye. Hun mener at ved å gi vanskelige vurderinger oppmuntres studentene til å jobbe hardere. Teorien hennes er at den første testen fungerer som en slags “vekkerklokke” for studentene. Når de forstår hvor vanskelig klassen faktisk er, vil de jobbe hardere til den andre testen og få bedre karakter. Stemmer dette? For å teste dette åpner vi chico.csv-filen inn i jamovi, se Tabell 10.2.

Datasettet chico inneholder tre variabler: en id-variabel som identifiserer hver student i klassen, variabelen grade_test1 med antall prosent riktig på den første testen, og variabelen grade_test2 med antall prosent riktig på den andre testen.

Tabell 10.2. Dr. Chico sin datafil med resultater på før- og ettertesten

id	test1	test2
student1	42.9	44.6
student2	51.8	54.0
student3	71.7	72.3
student4	51.6	53.4
student5	63.5	63.8
student6	58.0	59.3
student7	59.8	60.8
student8	50.8	51.6
student9	62.5	64.3
student10	61.9	63.2
student11	50.4	51.8
student12	52.6	52.2
student13	63.0	63.0
student14	58.3	60.5
student15	53.3	57.1
student16	58.7	60.1
student17	50.1	51.7
student18	64.2	65.6
student19	57.4	58.3
student20	57.1	60.1

Når vi ser på dataene virker det som om klassen virkelig er vanskelig (de fleste karakterene ligger mellom 50% og 60%), og det er ikke opplagt at det er en forbedring fra den første til den andre prøven.

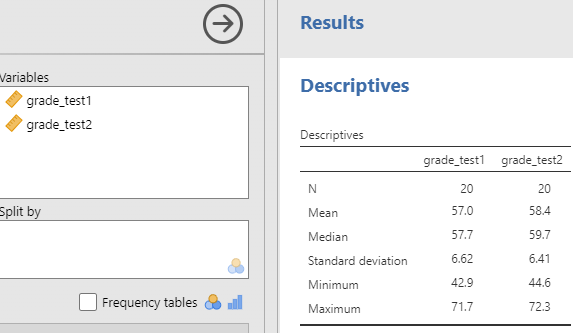
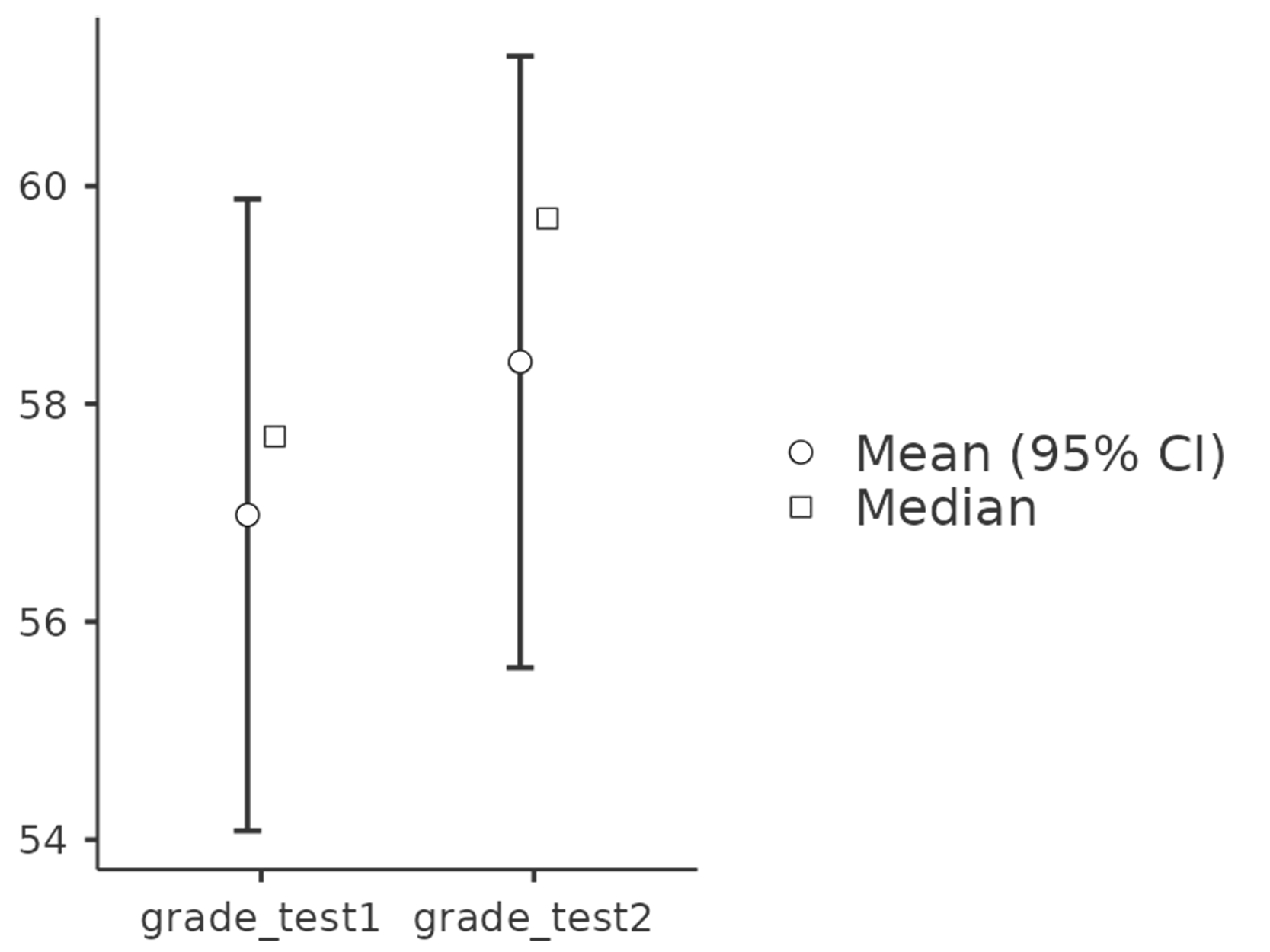
Tar vi en rask titt på den deskriptive analysen i Figur 10.7 (a) får vi forsterket inntrykket av at det ikke er en opplagt forbedring. Blant alle 20 studenter er gjennomsnittskarakteren 57% for den første testen og 58% for den andre testen. Men gitt at standardavvikene er henholdsvis 6,6% og 6,4%, kan det virke som om man lett kunne fått disse resultatene også hvis det ikke var noen effekt. Og inntrykket er det samme hvis vi visualiserer gjennomsnittene og konfidensintervallene, slik som i Figur 10.7 (b). Hvis vi skulle stolt på denne figuren og bredden på disse konfidensintervallene, ville vi lett ha trodd at forbedringen i studentenes prestasjoner kunne være tilfeldige.

(a) Deskriptiv statistikk for variablene

(b) Gjennomsnitt og 95% konfidensintervaller for variablene

Figur 10.7. Deskriptive analyser for de to variablene i chico-datasettet.

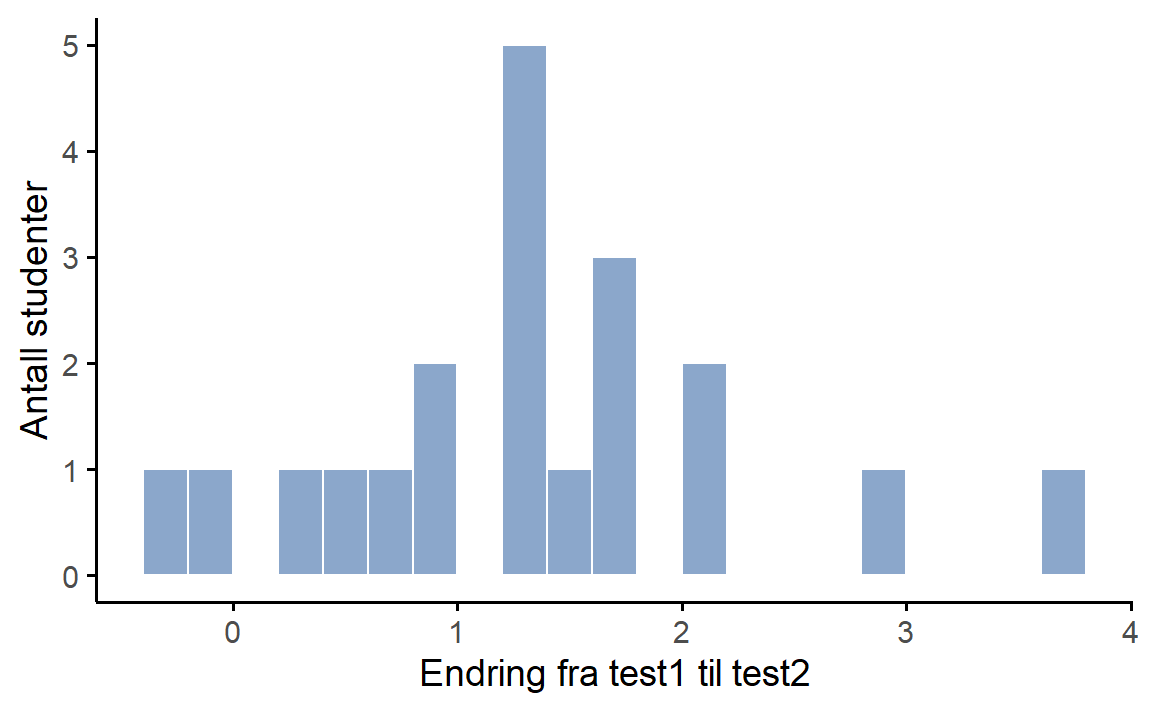
Men dette inntrykket er feil! Grunnen er at vi kun har vist statistikk og grafer som ikke tar hensyn til at samme person har avlagt en før- og en etter-prøve. Vi har regnet ut gjennomsnittet for førtesten og ettertesten helt separat, og dette vil være en fin analyse hvis det er helt forskjellige folk som tar før-testen og etter-testen, men i vårt eksempel er det de samme studentene. For å illustrere at studentene faktisk har en fremgang kan vi regne ut hver students endring fra test 1 til test 2, altså regne ut differansen \text{endring} = \text{grade\_test2} - \text{grade\_test1} og legge den til i datasettet. Jeg har visualisert denne variabelen i Figur 10.8. Når vi ser på histogrammet blir det helt klart at det er en reell forbedring her. Det store flertallet av studentene scoret høyere på test 2 enn på test 1, noe som reflekteres i at nesten hele histogrammet ligger over null.

Figur 10.8. Histogram som viser studentenes endring fra test 1 til test 2.

Derfor trenger man en paret t-test. Man kunne sett for seg at man regnet ut en ANOVA med to grupper før og etter, men dette ville ikke tatt hensyn til at samme student befant seg i hver gruppe.

10.2.2 Nullhypotesen og alternativhypotesen

Nullhypotesen for en paret t-test er

H_0: gjennomsnittlig endring mellom de to testene er null, altså: \text{endring} = 0

Alternativhypotesen er

H_1: gjennomsnittlig endring mellom de to testene er ulik null, altså: \text{endring} \neq 0.

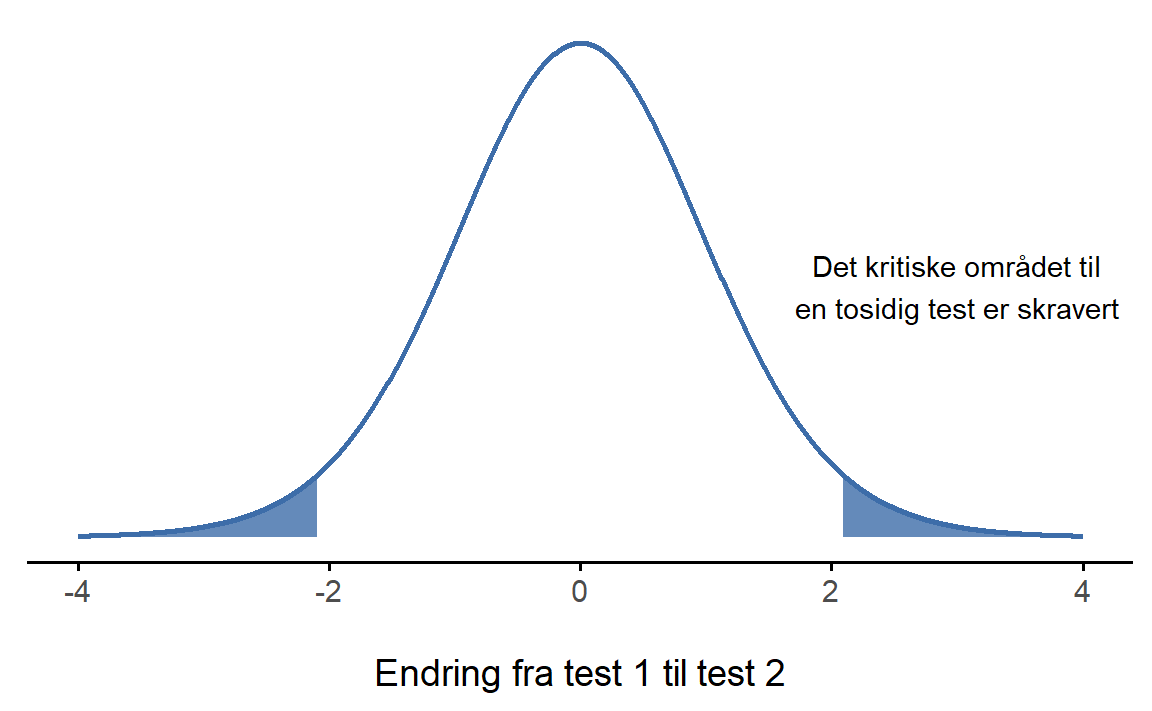
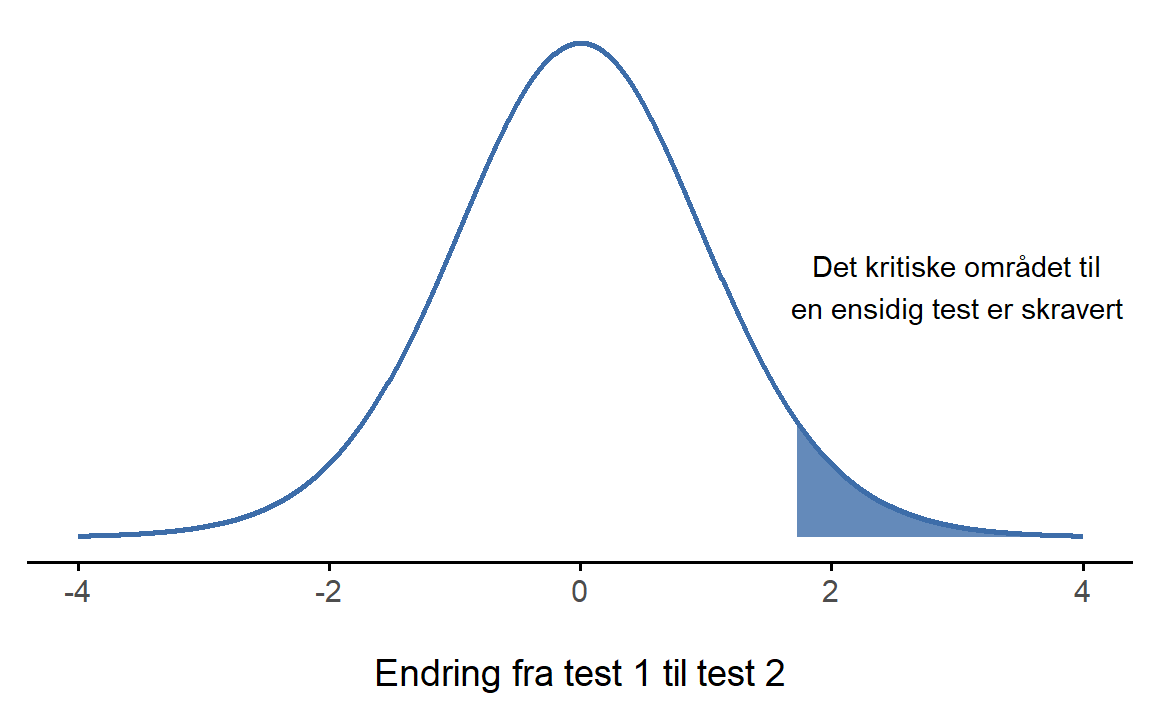
Paret t-test gjøres ofte med en ensidet test, se Seksjon 8.4.3. For Dr. Chico, som tenkte at studentene ville få til mer på test 2, blir hypotesene:

H_0: Gjennomsnittlig endring mellom de to testene er null eller negativ, altså: \text{endring} \leq 0

H_1: Gjennomsnittlig endring mellom de to testene er positiv, altså: \text{endring} > 0

10.2.3 Testobservatoren t og dens utvalgsfordeling

Nå skal vi konstruere en passende test. Løsningen er ganske enkel, siden vi allerede har gjort det meste av arbeidet tidligere. I stedet for å analysere grade_test1 og grade_test2 hver for seg, undersøker vi om endringsvariabelen grade_test2 - grade_test1 er ulik null.

Hvis studentene er plukket tilfeldig fra en populasjon, vet vi fra sentralgrenseteoremet, Seksjon 7.3.3, at endringsvariabelen er normalfordelt. Derfor er testobservatoren vår normalfordelt … nesten. Det eneste problemet er at vi ikke vet standardavviket til denne normalfordelingen, så den må estimeres. Dette gjør at testobservatoren vår er ekstremt lik normalfordelingen, men er bittelittegranne mer spredt fordi vi også må estimere standardavviket fra dataene våre. Den fordelingen som tar høyde for dette er t-fordelingen, så testobservatoren vår er t.

(a) Sammenlikning av t-fordeling og normalfordeling. t-fordeling er litt mindre presis, som vist ved at halene er bittelitt tykkere, altså at store verdier er vanligere.

(b) Forkastningsområdet til en tosidig t-test

(c) Forkastningsområdet til en ensidig t-test

Figur 10.9

Og det er faktisk alt! Konseptet er veldig enkelt. Trikset er å gjenkjenne når en parvis test er passende, og forstå hvorfor den er bedre enn en ANOVA i slike situasjoner.

Advarsel

Jeg har gjennom dette kapittelet sammenliknet paret t-test med ANOVA. De fleste lærebøker sammenlikner paret t-test med “vanlig” t-test. Jeg har valgt å ikke presentere den vanlige t-testen siden den er identisk med ANOVA når man har 2 grupper. Vi har altså spart oss fra å lære én test uten å tape noe.

10.2.4 Å gjøre testen i jamovi

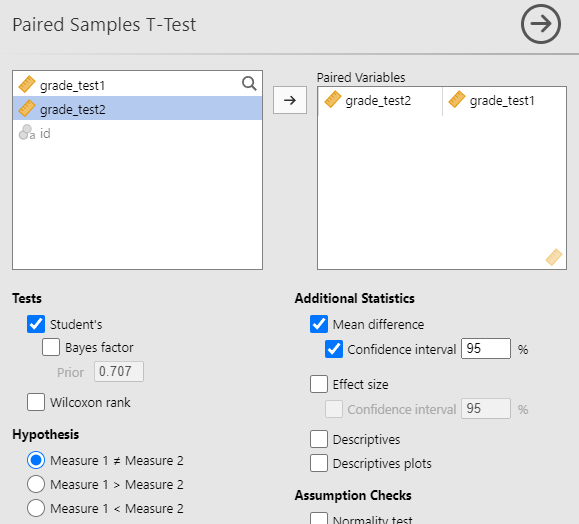
Du finner jamovi sin funksjon for paret t-test under “T-tests” → “Paired samples t-tests”. Jeg valgte innstillinger som i Figur 10.10 (a) og fikk resultatet i Figur 10.10 (b).

(a) Innstillingene for testen i jamovi

(b) Resultatene fra jamovi

Figur 10.10. Resultater som viser en paret t-test i jamovi.

Vi ser at resultatet er statistisk signifikant, og man kan rapportere det slik:

Endringen fra test 1 til test 2 var statistisk signifikant, t(19) = 6{,}48, p < 0{,}001. Gjennomsnittlig forskjell fra test 1 til 2 var 1,40 95% CI [0,951; 1,86].

Man bør tenke over om forutsetningene for testen er oppfylt i dette tilfellet. Dr. Chico valgte ikke studentene tilfeldig fra en definert populasjon; hun valgte ganske enkelt alle studentene som tok faget hennes. Dr. Chico ønsker nok å generalisere til populasjonen over studenter som tar kurset sitt, ikke bare dette året, men alle år hun underviser det. Hun kan argumentere for at akkurat hvilke studenter som tok faget hennes dette året er ganske tilfeldig, slik at man kan betrakte studentene dette året som tilfeldig trukket. Er du enig i det? Det er ikke en helt usannsynlig antagelse, men det er viktig å tenke over om antagelsene virkelig er oppfylte og hvilke konsekvenser det eventuelt får om de ikke er det.

I menyene i jamovi er også det muligheter for å velge ensidige tester. Akkurat i Dr. Chico sitt tilfellet blir resultatet det samme, men ensidige hypotesetester er sterkere og vil noen gange kunne forkaste nullhypoteser som tosidige hypoteser ikke kan.

10.3 Sammendrag

Her er hovedtemaene vi har dekket i dette kapittelet:

• For både ANOVA og paret t-test har vi lært
  • Når de kan anvendes
  • Hva nullhypotesen og alternativhypotesene er
  • Ideen bak testobservatorene, henholdsvis F og t.
  • Hvordan man utfører testen i jamovi

Det viktigste som ikke er dekket er ulike forutsetninger for når man kan benytte testene. Noen av disse forutsetningene er ganske tekniske, så det vil være vanskelig å inkludere dem i et kurs på dette nivået. Den viktigste forutsetningen er at det bør være et enkelt tilfeldig utvalg fra en populasjon, hvis ikke kan det bli vanskelig å tolke testene.

Navarro, D., & Foxcroft, D. (2025). Learning Statistics with jamovi: A Tutorial for Beginners in Statistical Analysis (1st ed.). Open Book Publishers. https://doi.org/10.11647/OBP.0333

---

1. Hvis du husker tilbake til Seksjon 7.3.3 så var standardfeilen standardavviket til en observator, i dette tilfellet gjennomsnittet, så disse standardfeilene angir hvor mye vi estimerer at gjennomsnittene vil variere hvis vi gjør studien mange ganger.